Democrat Senator Durbin Questions Freedom of the Press

On Fox News Sunday, Democrat Senator Dick Durbin of Illinois questioned whether bloggers were protected by the 1st Amendment under freedom of the press.  Let us re-read the 1st Amendment of the Constitution and see if his doubts about the rights of bloggers to write as an exercise of their freedom of conscience makes any sense at all.

Congress shall make no law respecting an establishment of religion, or prohibiting the free exercise thereof; or abridging the freedom of speech, or of the press, or the right of the people peaceably to assemble, and to petition the Government for a redress of grievances.

The breadth of this amendment as a means to allow individuals to use their minds, to produce their own ideas, and to make those ideas known to others is the unifying theme of this amendment.  Most people at the time of its adoption believed that this amendment guaranteed a broad freedom of conscience.  Certainly Thomas Jefferson and James Madison thought so.

When the amendment was written, the written word could only be distributed to others by using a rather expensive invention, the printing press.  But note that the amendment also allowed people to speak freely, to assemble and share ideas, and to complain to or seek reforms by the government.  In this context, it is not possible to believe that the 1st Amendment was only intended to allow those who distributed their ideas using a printing press to exercise their freedom of conscience.  I do not see the People then as thinking that freedom of the press was something that belonged only to someone who had made an investment in a printing press.  The core idea of the 1st Amendment was to allow people to use their minds and to share their ideas with others.

No, it seems very clear that the dissemination of an individual's ideas and thoughts by right was to be broadly protected by this amendment.  That being the case, the freedom to write down one's ideas and to disseminate them was to be protected from any abridging acts of Congress.  Thus, the right of bloggers to write down their ideas and to make them available to others for reading is clearly protected by the 1st Amendment.

With experienced Senators such as Dick Durbin showing such profound ignorance of the 1st Amendment, it is no wonder our government has become such a constant threat to the rights of the individual to life, liberty, property, the ownership of one's own body, mind, and labor, and to the pursuit of personal happiness.

To be sure, there is considerable evidence that Dick Durbin is less ignorant than a man of evil intent.  He, like all socialists, is only too happy to mislead the many who are uninformed about their individual rights.  Persons asserting their individual rights are necessarily a major problem for the supporters of Big Government and socialism.

Responding to a Progressive Elitist University Request for Donations

A Brown University student of the Class of 2015 sent me an e-mail request for a donation to the university from which I earned my Sc.B. in Physics degree in 1969.  Because of the magnitude of the tragedy that Brown has so failed to provide young and bright students with an adequate education, I took the time to write the following response:

It is precisely because far too many faculty, staff, and students at Brown University view themselves as "partners and agents for collective social change" that I am deprived of the pleasure of supporting a real education at Brown.  They share the image of themselves as Progressive Elitists justified fully in the use of governmental force to impose values on a largely immoral or amoral people.  They wish to micromanage the lives of millions of people they do not know, yet consider incompetent to manage their own lives.  They ignore the essential fact that people are complex and highly differentiated in character, life circumstance, and values.  They seek an easily acquired sense of intellectual and moral superiority, while abrogating to themselves power and money taken by force.

A real education would encourage students to see how honoring the equal, sovereign rights of the individual to life, liberty, property, the ownership of one's own body, mind, and labor, and the pursuit of personal happiness is the real path to achieving the general welfare.  This education would illustrate the need for a legitimate government whose only purpose was the support of these individual rights and which would never seek to harm some while claiming it was helping the majority or some favored minority.  A real education would make it clear that a government that forces some or many to serve the interests of others is tyranny and disruptive of the real benefits of life in a society.  It would show how those benefits flow from the incredible richness of choices and freedom of action when all of our relationships are freely chosen for our mutual benefit.  It would honor freedom of conscience and of association, rather than crippling these freedoms as the big government approved by most at Brown University does.  These freedoms are critical to man who must live by the use of his mind.  An education is supposed to aid man in developing the rationality and analytical capability of that mind.

Unfortunately, any money I give to Brown is used mostly to deprive me and those I love of our individual rights.  It is used to increase the level of already exorbitant tyranny in the Land of the Free.  It is used to diminish the many wonderful advantages of living among others willing to engage in a free trade of ideas, goods, and services.  It creates a government so complex that the vast majority of citizens cannot understand what it is doing and how to control it.  They become pawns due to their limited time, money, and intellect to those few Progressive Elitists who actually do control government to some degree.  But just as the slave master was enslaved by his slaves, so are the Elitists enslaved by the ignorant or insufficiently informed people they think they control.

Soon, as is the case now, control of government is really in the hands of haphazard and conflicting special interest groups (factions in the terms of the founders), who step in and take what they want at the expense of everyone else.  A few of these special interests or factions:

• Crony mercantilists such as green energy companies,
• GE, GM, Chrysler, Boeing with its Export Bank subsidies,
• farmers with crop supports,
• students taking government student loans,
• faculty taking government funded research grants,
• labor unions forcing workers to pay them dues and buying politicians' votes, while systematically underfunding worker pension plans,
• radical environmentalists claiming that economic development is the enemy even as developed countries do most to clean their environments,
• global warming alarmists falsely accusing user's of fossil fuels of overheating the planet,
• people faking disabilities by the millions,
• millions on unemployment benefits for years,
• big bankers and stock investors happy to see the Federal Reserve flood the economy with devaluing printed money,
• home buyers buying homes they cannot afford with government encouragement,
• insurers happy to see people forced to buy health insurance they cannot afford for coverage they do not need as the government asserts its ownership of our very bodies,
• millions happy to use food stamps and other welfare rather than take a job,
• those who use government licensing to keep others out of their profession, 
• a huge government-run education establishment dominated by pro-big government propaganda, teachers unions, and mediocrity,
• large companies that seek to cripple smaller companies with a myriad unintelligible regulations, and of course
• the many power-hungry and corrupt politicians who populate both major parties, though especially the one most favoring the accelerating growth of government.

I had the independence of mind and the knowledge of history, economics, civics, business, and science to withstand the many pressures at Brown to conform to the Progressive Elitist viewpoint that the brutal use of force to accomplish their goals was justified by the claimed purity of those goals.  Of course, kings and aristocrats of old, slave owners, fascists, and communists all made very similar claims.  The end result for any society that deprives its individual citizens of their rights is all too well-known and can be ignored only by the ignorant or the malevolent.

Being a small business owner who has repeatedly converted his limited retirement funds into capital to keep his independent laboratory going through this government caused and government maintained recession of five years duration, my charity activity has to be carefully directed to those fighting the critical battle of our time, indeed of all time.  I am supporting the Competitive Enterprise Institute, the Cato Institute, the Atlas Society, the Institute for Justice, the Club for Growth, the Tea Party movement, the NFIB, and the Right to Work Committee.

Brown University is not very competitive given its concerted deception and propaganda exercised on young minds, too many of which are weak.  It gives me no pleasure to say this, since it is a huge tragedy that Brown is not performing the great service it should be and could be doing.

Maryland Gun Control Infringement of the Right to Self-Defense

Oh, the many pleasures of corresponding with one's representatives in the state legislature and the federal government as an exercise in the right to petition one's grievances ends only in frustration.  One can always count on a Progressive Elitist standard viewpoint from these representatives, at least in the most un-free state of Maryland, known most erroneously as the Free State.  This state, long ago, provided perhaps the best unit to fight in the American Revolutionary War.  At that time, there sure was no prohibition against owning a military-style weapon.

The Progressive Elitists of Maryland are most united in the belief that while one may have a right not have one's hunting rifle prohibited, a weapon designed for self-defense is to be absolutely prohibited.  In this Progressive Elitist viewpoint, no infringement means only that any barrier an individual should have to overcome to exercise a right must not amount to an absolute prohibition, except in some cases.

This is the response I received to my letter in opposition to the latest effort of the state of Maryland to infringe the right to bear arms from my delegate Anne Kaiser in the Maryland House of Delegates:

Thank you for writing to my office and voicing your opposition to SB281:  Firearm Safety Act of 2013, introduced by Senate President Mike Miller on behalf of Governor Martin O’Malley.  This legislation provides a comprehensive plan of reforms to make people safer and reduce preventable gun violence.  It includes provisions regarding gun licensing and fingerprinting; gun safety; and mental health safeguards and services.

Specifically, the provisions of SB 281 bans the sale of military-style assault weapons; limits magazine capacity to 10 rounds (the previous limit was 20) and requires licensing, fingerprinting, and safety training to purchase a handgun.  These provisions should reduce “straw purchases” (where someone with a record gets a friend to buy a gun on their behalf) of both assault style weapons and handguns which over time should reduce the number of illegal guns on our streets while also promoting sensible, responsible gun ownership.

Further, this initiative creates safeguards to keep guns away from people who may be a danger to themselves or others due to mental illness, while also facilitating unprecedented levels of information sharing among federal and state partners for background checks.  This bill improves mental health services in Maryland by establishing a Center for Excellence on Early Intervention for serious mental illness and expands Maryland’s Crisis Intervention Teams, Crisis Response Services, and Mental Health First Aid.  Also, this bill establishes a Department of Health and Mental Hygiene led Task Force to Improve Continuity of Care for Individuals in the Community Mental Health System.

Despite characterizations of this bill and those of us who voted for it, I fully support our 2^nd amendment rights.  I place our right to bear arms right alongside our freedom of speech, of a free press and our freedom of religion.  With each of these guaranteed freedoms comes rights and with each right comes responsibility.  And with each responsibility, comes reasonable regulations.

I believe that this bill crystallizes that responsibility in important, meaningful and manageable ways.  Crucially, the new law does not do the following:  it does not prohibit lawful citizens from obtaining or owning a handgun and it does not require additional licensing procedures for hunting rifles and shotguns.  The new law does not force citizens who lawfully possessed an assault weapon prior to the bill’s passage to surrender their weapon or to register it.  Furthermore, it does not require current lawful gun owners to retroactively obtain a license.

Your views are important to me and I appreciate that you have taken the time to write to me.  Please do not hesitate to contact me during the session should any other concerns arise.

 Very truly yours,

 Anne R. Kaiser

The exercise of a right comes with only the responsibility not to violate the equal sovereign rights of other individuals.  It does not come with a responsibility to expend time and effort to prove that one has such character as may be in popular approval by the government.  I should not have to prove that I will not somehow and at some future date violate the rights of others.  As for gun safety, if I already know that (as a veteran), why should I have to take a course from some state-licensed safety instructor at great expense and at the cost of valuable time?  This is an example of the state very much infringing my right to self-defense.

The 2nd Amendment clearly says the right of the people to keep and bear arms shall not be infringed.  Note that no infringement means that there shall be no barriers.  It does not mean that the barriers are such that they can be overcome and are not absolute prohibitions.

Furthermore, the prohibition on military style weapons makes no sense whatever.  The most essential reason one has a right to arm oneself for is self-defense.  Both the prohibition against so-called military style weapons and the limit to 10-round magazines are fundamental infringements on the right to self-defense.  The military uses the weapons it uses for defense.  I would use any weapon I might have for defense.  The reason we have a military is simply as an extension of our individual right to self-defense and the fact we have a military does not deprive us of any part of our right to self-defense.  Note also that this is an explicit prohibition and not a barrier which can be overcome with sufficient effort.

It is noteworthy that Anne Kaiser claims that she holds the right to bear arms as dearly as freedom of speech, freedom of the press, and freedom of religion.  Logically this means that the exercise of these critical freedoms can also be infringed by the requirement to be fingerprinted, forced to take lessons in their safe use, and that many statements and beliefs can be prohibited so long as some are allowed with due licensing of the individual.  In fact, Kaiser explicitly claims that the state can regulate freedom of speech, press, and religion.  Perhaps initially only the mentally ill and felons will be denied the license to exercise freedom of speech, the press, and religion, but I am sure we can count on the Progressive Elitists to expand the class of people denied these rights with time.

Of course, in the eyes of the Progressive Elitist, a person of the Tea Party persuasion is mentally ill.  Many of them have said this explicitly.  Since most psychiatrists seem to be Progressive Elitists, the state will have no problem finding one who will attest that someone who challenges the power of unlimited government is suffering a mental problem.

According to the National Institute of Mental Health, 26.2% of the U.S. population has a diagnosable mental disorder in a given year.  Does this mean that the state of Maryland will deny licenses to 26.2% of the applicants because they are claimed to have a mental illness?  Probably not, since most such cases have not been diagnosed, but given the infringements of this bill, will one have to have extensive testing for mental illness before being licensed in the near future.  After all, a precedent will have been established.  How extreme and of what type must the mental illness be before one is denied a license?  Yes, she talks of being a threat to oneself or others, but this is pretty speculative stuff and does not the Precautionary Principle so beloved by the Progressive Elitists require a very low bound on the possibility of danger?  If one were ever diagnosed as having a mental illness, would one be forever denied a license to bear arms?  Given how dear the right to bear arms is for Anne Kaiser, how long before the same problems arise to get that license for the exercise of freedom of speech?  You must have much more faith in the goodwill of government than I do to feel at all comfortable with these issues.  Ignorance of history or total irrationality would be a precondition for such faith.

As for the new mental health bureaucracy this law will set up in the state of Maryland, I can only imagine the horrors to come.

It is comforting to know that more than half the number of votes needed to pass this bill in the Maryland House of Delegates may have been cast by the 26.2% of the delegate population with diagnosable mental illnesses.  The remainder of those for this bill may have been voted into office with most of the votes from the 26.2% of Maryland voters who are estimated by the very Progressive Elitist National Institute of Mental Health to have diagnosable mental illnesses.  To be sure, such mental illnesses may be far more common among the Maryland Delegates than among the population at large.

The violation of individual rights by the state of Maryland and by the federal government has become a habit.  There is nothing one can trade one's basic individual rights for that is worth the trade.  You should note that the Declaration of Independence informs us that the only legitimate function of government is the protection of individual rights.  Governments that violate those rights become morally illegitimate no matter how many popular votes the politicians may collect.   Evil thrives in the state of Maryland because collectivist politicians here collect hordes of votes.

The Maryland House of Delegates is coming to help us exercise our responsibilities.  Be afraid ...  no, be terrified!

Job Creation Remains Stagnated - 4.33 years of Stagnation

Almost all reports about the April unemployment numbers have been positive.  It is easy to see why people are grasping at straws given the bleak employment situation of the last four years and more.  But, a rational analysis of that situation shows it to continue in all due bleakness.  Let us observe the long term record of missing jobs based upon the percentage of the non-institutional working age population that chose and could find jobs in January 2000.  Jobs were plentiful and comparatively enticing then.  Now, not nearly so much.

The missing jobs record is shown below, based on the household survey without seasonal adjustment:

Given the record of false cost of living reporting by the government, I have been loathe to accept their seasonally adjusted employment figures for both lack of trust in their honesty and because in such extraordinary employment conditions over such a long time, it would be difficult to develop a good algorithm for the seasonal fluctuations.  So, we will need to compare April 2013 with April of 2012, 2011, and 2010 to see how the economy is doing in providing jobs.  There is only the very barest improvement since April 2012, but the number of missing jobs compared to April 2011 is virtually identical!  Worse yet, April 2010 had fewer missing jobs than the Aprils of 2011, 2012, and 2013!

This story of no improvement beyond just keeping pace with population growth, but not actually replacing the lost jobs of the deep government-induced credit collapse of 2008, has been the consistent story for 4 and one-third years now.  This has been a most extraordinary recession - - induced by government and maintained adamantly by government.

The employment record is given in detail in the table below:

Now let us compare the percentage of missing jobs, rather than the absolute number of missing jobs, for the months of April from 2010 through 2013.  Respectively, we see the real unemployment rate was 13.03%, 13.47%, 13.34%, and 13.14% for these April months.  This is pretty much as much stagnation as one can get.  Yes, the April jobs situation is not as bad as it was in March, but then in every one of the last four Aprils this has been true.  It is just part of the seasonal fluctuation in jobs.

There has been no headway in reducing the number of Americans who are working part-time for economic reasons.  In April 2012 there were 7,694,000 such unwilling part-time workers.  In April 2013, there are 7,709,000 such unhappy workers.  Far from a reduction in the high part-time work percentages created by the recession, there has actually been a small increase of 15,000 part-time workers.

In addition, there has been an increase in the number of persons working part-time for non-economic reasons, such as attending college.  These numbers have increased from 19.443 million in April 2012 to 19.829 million in April 2013.  This increase of 386,000 in part-time workers for non-economic reasons according to the Bureau of Labor Statistics classification does not necessarily mean that the reasons actually are non-economic.  In many cases, someone may be going to school rather than working because they otherwise think they cannot find a job.  Or, they may be taking care of a sick relative or children rather than paying someone else to do it, because they cannot get a good enough job to be able to pay someone else.

There is good reason to believe that the looming train-wreck of ObamaCare is discouraging small businesses from hiring full-time employees and in some cases from hiring part-time employees as well.  So, part-time work is increasing, while full-time work is in stagnation at decidedly recession levels.

This complete jobs stagnation record over such a long period is definitely the result and responsibility of the Obama regime.  The American private sector has to be knocked down continuously to keep it from recovering.  Obama and his socialist thugs are only too committed to doing exactly that.  One of their amazing feats has been to keep the American people completely distracted from the abysmal job creation record during the Obama administration time in power.  Gun control, immigration reform, and the micro-reduction in the rate of increase in government spending due to the sequester have been played magnificently as distractions from the wreckage of the American economy.

What if the Atmosphere had no Greenhouse Gases?

According to the "settled science", the Earth's surface temperature would be about 33K or 33C colder on average than it is now if there were no so-called greenhouse gases.  The settled scientists treat the Earth's surface and its atmosphere as a single system which is in radiative equilibrium with the sun and space.  The Earth system is assumed to be a black body radiator and the calculated temperature of such a black body radiator is about 255K or about 33K colder than the approximate observed average temperature of 288K.  They forget to note that the Earth's surface temperature is about 288K, but the surface is not in radiative equilibrium with the sun and space.  Therefore, it is completely wrong to compare the average Earth surface temperature with the temperature of the equivalent effective black body radiator even if the Earth's surface were a black body radiator.

Let us dispense with the infrared active gases, the so-called greenhouse gases, so that the Earth's surface is in radiative equilibrium with the absorbed solar insolation and the infrared emissions into space.  In the greenhouse gas game, clouds are considered to cause part of the effect and this is natural given that without water vapor they would not exist.  Let us look at the Kiehl-Trenberth Earth Energy Budget of 1997, which the IPCC 4th Report of 2007 claimed was the settled science, to find a few numbers we will need to perform a simple calculation.

Fig. 1.  The Kiehl-Trenberth Earth Energy Budget of 1997, representing the settled science according to the IPCC 4th Report of 2007.

Now, I have found any number of faults with this diagram in previous posts.  But, given the claims of the settled science I am at least justified in throwing some of its consequences back at them.  In addition, a few of the numbers on certain factors ought to be about right, or they have spent about $140 billion of U.S. taxpayer money with unbelievable incompetence.

So, let us look at the energy inputs to the Earth's surface.  The average daily power input at the top of the atmosphere is 342 W/m^2.  The 77 W/m^2 that reflects off clouds does not do so, since we have taken the clouds away.  The 67 W/m^2 absorbed by the atmosphere is much reduced.  Ozone and even O2 to a small degree do absorb some of the energy.  Let us be generous in estimating how much is absorbed by the non-greenhouse gases and say they absorb 12% of the incoming sunlight, rather than the 19.6% of the K-T diagram above.  By being generous in this, we are lowing the radiation that will reach the surface to warm it.  So (12%/19.6%) 67 W/m^2 = 41 W/m^2 is still absorbed by the atmosphere and does not reach the surface.

Consequently, the solar radiation that does reach the surface is (342 - 41)W/m^2 = 301 W/m^2.  But now we note that not all of the radiation from the sun that is incident upon the surface is absorbed.  The fraction absorbed is (168/198) = 0.848 in the diagram.  If we assume the same fraction of the radiation incident on the surface is absorbed, then we have an absorbed power density in the surface of 0.848 (301) W/m^2 = 255 W/m^2.

Let us, after the style of the greenhouse gas catastrophe believers, apply the Stefan-Boltzmann Law for radiation, which is

P/A = ε σ T⁴,

in which P is the power in Watts, A is the absorbing or radiating area in square meters, σ = 5.6697 x 10^-8 W/m²K⁴ the Stefan-Boltzmann constant, T is the temperature in Kelvin, and ε = 1 (the emissivity) for the case of the black body radiator.

In this case, the Earth's surface is in radiative equilibrium with space because there are no gases in the greenhouse gas free atmosphere to absorb the thermal infrared radiation emitted by the Earth's surface.  Consequently, the black body surface absorbing 255 W/m^2 would be at a temperature of 259K, which is 29K colder than the approximate average temperature of 288K.

However, when pushed a bit, even the catastrophic man-made global warming alarmists concede that the Earth's surface is not a true black body radiator.  They say that the water and the organic materials that cover much of the Earth's surface all have an emissivity near 0.95.  They claim the Earth's surface emissivity is 0.95, nearly as high as that of a black body radiator.  Using that emissivity instead of that of the black body radiator of 1, the calculated temperature becomes 262.3K.  This is 25.35K colder than the best estimate for the Earth's average temperature, which is about 14.5C or 287.65K.

Physicists do not think of water, plants, and minerals as near black body radiators.   A black body radiator is supposed to have the property that it readily absorbs radiation of all wavelengths and emits radiation in a continuous spectrum.  It has to have a harmonic oscillator response at each and every frequency, both to absorb and to re-emit radiation energy.  In a black body cavity, the emissivity of a surface and the absorptivity must be equal.  Those who back the greenhouse gas hypothesis of strong back radiation and warming of the Earth's surface, claim that not only is the surface emissivity nearly that of a black body radiator, but that 100% of any back-radiation from greenhouse gases is absorbed by the surface.  In emission mode, the Earth's surface is either a black body emitter or nearly so, they say, and it is a black body absorber of the thermal infrared radiation emitted from the Earth's surface.

Real materials do not have excitable harmonic oscillator responses at all frequencies.  In fact, infrared spectroscopy has long taken advantage of the discrete and characteristic absorptions that different materials have to identify those materials.  We can use an infrared spectrometer to determine whether a material has water in it.  We use it to distinguish polypropylene from polyethylene, polystyrene, and cellulose.  It can be used to identify various sugars, starches, and proteins.  Yet, the climate alarmists often claim that organic materials all behave very much like black body radiators and absorbers, emitting and absorbing radiation at all frequencies, at least all thermal infrared frequencies.  Well, no they do not.

That the Earth's surface materials are not black body radiators and absorbers matters.  For instance, if the emissivity is calculated which would cause the Earth with no greenhouse gases to have an average temperature of 287.64K or 14.5C with the absorbed solar insolation average power density we calculated above of 255 W/m^2, then the emissivity would be 0.657.  Is this a plausible effective emissivity for the real Earth surface?  And note that if the surface emissivity is less than 0.657, then there have to be other cooling mechanisms to bring down the equilibrium radiative temperature which then would be higher than 14.5C.

Let us look at a portion of the Earth's radiative output according to the IRIS satellite looking down on the dry Sahara Desert in the figure below.  Note that both at the low wave number end and the high wave number end this spectrum is truncated.  It is truncated at the low wave number end because most infrared spectrometers use window and other materials which absorb too much infrared radiation at lower wave numbers.  There are specialized near infra-red instruments that can make measurements in that lower number range by using different materials.  I do not know why this spectrum is cut-off at the larger wave number end.  My infrared spectrometer acquires spectra from 400 to 7800 wave numbers.  Customarily, we cut our spectra off at 4000 wave numbers, because we almost never see any absorptions in materials between 4000 and 7800 wave numbers.  This figure also presents a model that calculates infrared absorption by greenhouse gases, which curve is shown in red.  At the moment, we are not interested in this.

Fig. 2.  A portion of the infrared emission spectrum of the Earth in the Sahara Desert region as seen from space.  Note that the infrared behavior of materials in the Earth's surface from 400 to well beyond 1500 wave numbers is the wavelength of relevant response for these materials.  The satellite spectrometer measures power and does not actually measure the black body temperatures given by the dashed lines.

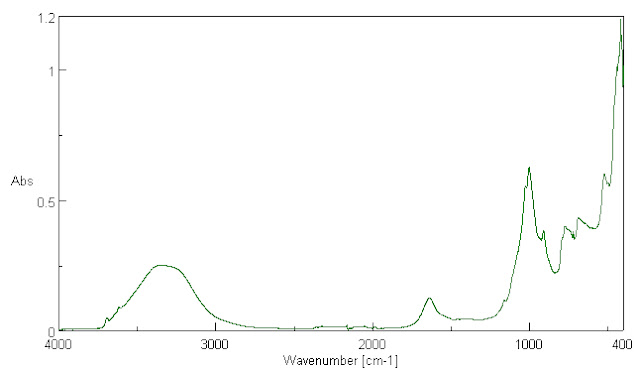
Since water covers about 70 to 71% of the Earth's surface, let us examine the infra-red absorption spectrum of water.  It is presented in Fig. 3.

Fig. 3.  The FTIR infrared absorption spectrum of tap water.  This is not the absorption spectrum of a black body absorber.

Let us assess this water spectrum.  First, the absorption from 4000 to 7800 wave numbers was zero.  Second, if we generously assume that the maximum absorption here at about 400 wave numbers is a wavelength at which water is sort of a black body absorber, then if at every other wavelength it absorbed the same amount of radiation, we might take this to indicate a material with an emissivity of 1 over these infrared wavelengths which are found in the same range as the emissions from the Earth.  Note that if CO2, whose main absorption is shown in Fig. 2, were causing radiation to be emitted from it back to surface water, the water absorption spectrum does not indicate black body absorption in the vicinity of 675 wave number.

In most other parts of the water spectrum the absorption is even lower.  The integrated area under the absorption curve compared to the area if absorption were everywhere from 400 to 4000 wave numbers equal to the maximum absorption is a fraction of 0.192.  The settled science of the global warming community says that the emissivity is equal to the absorptivity.  This is not actually true for non-black body materials, but if it were true for water, then it would be reasonable to think of this as the average emissivity over this range, and this is much smaller than 0.95.

Could it be that land material emissivities are gigantic and very black body like?  The greenhouse gas proponents claim it is for organic materials, such as plant life.  Let us examine a blade of green grass.

Fig. 4.  The FTIR infrared absorption spectrum of a green blade of grass.  Note that land surface temperatures are supposed to be made 1.5 meters above a field of grass.  This absorption spectrum is not that of a black body absorber.  Grass is full of water and the absorption peaks for water are clearly in this spectrum with some additional peaks due to the organic components in grass blades.

If we take the absorptivity of the green grass blade as one when the absorption across the range is equal to its maximum amount, then the ratio of the actual absorption to that is only 0.207.  A green leaf from a bush is similar, though slightly more absorbing by the maximum absorption criterion without taking into account the absolute absorbance from the spectrum.  The maximum peak absorbance for the bush leaf was less than that of the grass blade.

Fig. 5.  The FTIR infrared spectroscopy absorption spectrum for a green leaf from a bush.  As with a blade of grass, this leaf is full of water and the water peaks are all present.  

Taking the ratio of the actual infrared absorption to that if there were uniform absorption at the maximum value, the absorptivity is then 0.269.  This method should produce an upper bound on the absorptivity.  Then if we say as the greenhouse gas advocates do that the absorptivity equals the emissivity, we have an emissivity of less than 0.269.  Comparing this to the green grass blade, it is actually clear that the maximum absorption was lower for the bush leaf than for the blade of grass.  It is not really significant that the ratio value calculated is larger than that for the blade of grass.  What is important is that there is good reason to believe neither plant is even close to that of a black body radiator.

Is the story different for soil?  The FTIR infrared absorption spectrum follows:

 
Fig. 6. The infrared absorption spectrum of a moist and fairly rich soil.  The maximum absorption just above 400 wave number is actually very high, but the integrated absorption ratio to that of the constant absorption at the maximum rate is very low.

The soil spectrum has less water in it than the grass and bush leaf spectra showed.  If we most generously take the maximum absorption to be that of a black body radiator, the actual absorption is only 0.123 of that.  Again, if the emissivity were equal to this upper bound absorptivity level, than it would also be only 0.123.  Again, this is far short of 0.95.

Of course soil has both inorganic minerals in it and decayed plant materials.  Let us examine the infrared absorption spectrum of a feldspar mineral:

Fig. 7.  The FTIR infrared spectroscopy absorption spectrum of a mineral feldspar material.  This particular feldspar has sodium oxide, potassium oxide, aluminum oxide, and silicon dioxide in three different chemical phases.  Two of the phases are significantly hydrated.  This then is an example of a complex mineral of a type fairly common in the Earth's crust.

Relative to the strongest absorption peak, the absorptivity overall in this range of the infrared spectrum is about 0.117.  If the emissivity were equal, it would not be greater than 0.117 also.

Finally, let us consider a common, but simple mineral, sand:

 Fig. 8.  The infrared absorption spectrum of dry sand is shown.  The strongest absorption peak is actually very weak compared to those of the other materials considered.

Treating the strongest peak as locally the equivalent of a black body radiator is surely wrong.  Give this peak all the spinach you want and it will not become black body radiator like!  This is a weakly absorbing peak.  But, again being otherworldly generous, if it were the level of absorption of a black body radiator, this sand would have an absorptivity of no more than 0.098.  This is about an order of magnitude lower than the Earth surface emissivity claimed by greenhouse gas supporters to be 0.95.

In another post, I found the Earth's effective surface emissivity to be between about 0.45 and 0.50.  Because the absorptivity values in the infrared spectra I have given above are so low, either the emissivity values are significantly higher than the absorption values or there would appear to be a problem.  Now while the emissivity values can be higher for a non-black body material, much of the explanation is found in another simple matter which has been overlooked by the incredibly well-funded settled scientists of the greenhouse gas theory.

The power density side of the Stefan-Boltzmann equation P/A = ε σ T⁴, uses a very simple and gross idea of area.  The square meter is defined by a square with sides of 1 meter each.  But when the Earth is radiating from a grassy field, the radiating surface area is not 1 square meter inside that square with sides of 1 meter length.  The relevant emitting surfaces are the area of every blade of grass and any exposed soil between the blades of grass.  The emitting surface area may be 2 or 2.5 times the nominal area of 1 square meter of ground.  Even the sandy beach will have the surface area given by following the surface area of every grain of sand.  Surely there is emission from the ground under the tree, the trunk, the branches, and the leaves in many land areas.  Even the oceans will have maybe 1.2 times the emitting surface area of the nominal square which is used on the power side of the radiation equation due to waves and ripples.  

The energy the surface absorbs from the sun is distributed to some depth in the oceans or into the soil or rock surface on land.  The heat absorbed on average each day is far more reasonably provided by the simple 1 meter by 1 meter average power density provided by the sun.  But that energy is then also supplied to each bit of infrared radiation emitting surface area as the emission depletes the stored energy in the surface and the near surface.  Thus, effectively, the area on the right side of this Stefan-Boltzmann equation representing surface emission is almost always larger than the area on the left side taken to represent the area of solar insolation absorption.  Most surfaces on the Earth surface will definitely have a larger emitting surface area.  This has the effect of multiplying the emissivity of the emitting material by the ratio of the greater surface area emitting.  The ratio of the emitting surface area to the solar radiation area is multiplied times the normal laboratory measured emissivity of the emitting material.  The increase in the effective emissivity of the Earth surface is substantial.

Now note that the greenhouse gas claim that infrared absorbing gases cause a very large increase in the Earth's surface temperature is based on a claim that the emissivity of water and plants is 0.95 or even 1.0.  If this were so, then this observation of the need to account for the greater emitting surface area would create a whole different problem for their theory.  What they claim is a measured 0.95 emissivity for water would become a super black body emitter with an effective emissivity of say (1.2)(0.95) = 1.14 due to the waves of the ocean increasing its emitting surface area.  The situation over the prescribed grassy field for land surface temperature measurements would be even worse.  One might easily have an emitting area two times the nominal square area, so the grassy surface emissivity would be 2 (0.95) = 1.9.  Imagine all of that radiation converging on their temperature station only 1.5 meters above this super, super black body radiator!

This conclusively demonstrates that it is very plausible based on laboratory spectra on the materials from the surface of the Earth that the effective emissivity of the surface of the Earth is less than 0.5.  Any effective Earth surface emissivity less than 0.657 as I showed means that there is no warming effect due to the so-called greenhouse gases. Indeed, an effective Earth surface emissivity of less than 0.5 is consistent with a net cooling effect due to the infrared active gases of water vapor, carbon dioxide, methane, and nitrous oxide.  I have stated elsewhere why this is what we should expect.  I will write more about this in the near future.