Let us dispense with the infrared active gases, the so-called greenhouse gases, so that the Earth's surface is in radiative equilibrium with the absorbed solar insolation and the infrared emissions into space. In the greenhouse gas game, clouds are considered to cause part of the effect and this is natural given that without water vapor they would not exist. Let us look at the Kiehl-Trenberth Earth Energy Budget of 1997, which the IPCC 4th Report of 2007 claimed was the settled science, to find a few numbers we will need to perform a simple calculation.
Fig. 1. The Kiehl-Trenberth Earth Energy Budget of 1997, representing the settled science according to the IPCC 4th Report of 2007.
Now, I have found any number of faults with this diagram in previous posts. But, given the claims of the settled science I am at least justified in throwing some of its consequences back at them. In addition, a few of the numbers on certain factors ought to be about right, or they have spent about $140 billion of U.S. taxpayer money with unbelievable incompetence.
So, let us look at the energy inputs to the Earth's surface. The average daily power input at the top of the atmosphere is 342 W/m^2. The 77 W/m^2 that reflects off clouds does not do so, since we have taken the clouds away. The 67 W/m^2 absorbed by the atmosphere is much reduced. Ozone and even O2 to a small degree do absorb some of the energy. Let us be generous in estimating how much is absorbed by the non-greenhouse gases and say they absorb 12% of the incoming sunlight, rather than the 19.6% of the K-T diagram above. By being generous in this, we are lowing the radiation that will reach the surface to warm it. So (12%/19.6%) 67 W/m^2 = 41 W/m^2 is still absorbed by the atmosphere and does not reach the surface.
Consequently, the solar radiation that does reach the surface is (342 - 41)W/m^2 = 301 W/m^2. But now we note that not all of the radiation from the sun that is incident upon the surface is absorbed. The fraction absorbed is (168/198) = 0.848 in the diagram. If we assume the same fraction of the radiation incident on the surface is absorbed, then we have an absorbed power density in the surface of 0.848 (301) W/m^2 = 255 W/m^2.
Let us, after the style of the greenhouse gas catastrophe believers, apply the Stefan-Boltzmann Law for radiation, which is
P/A
= ε σ T4,
In this case, the Earth's surface is in radiative equilibrium with space because there are no gases in the greenhouse gas free atmosphere to absorb the thermal infrared radiation emitted by the Earth's surface. Consequently, the black body surface absorbing 255 W/m^2 would be at a temperature of 259K, which is 29K colder than the approximate average temperature of 288K.
However, when pushed a bit, even the catastrophic man-made global warming alarmists concede that the Earth's surface is not a true black body radiator. They say that the water and the organic materials that cover much of the Earth's surface all have an emissivity near 0.95. They claim the Earth's surface emissivity is 0.95, nearly as high as that of a black body radiator. Using that emissivity instead of that of the black body radiator of 1, the calculated temperature becomes 262.3K. This is 25.35K colder than the best estimate for the Earth's average temperature, which is about 14.5C or 287.65K.
Physicists do not think of water, plants, and minerals as near black body radiators. A black body radiator is supposed to have the property that it readily absorbs radiation of all wavelengths and emits radiation in a continuous spectrum. It has to have a harmonic oscillator response at each and every frequency, both to absorb and to re-emit radiation energy. In a black body cavity, the emissivity of a surface and the absorptivity must be equal. Those who back the greenhouse gas hypothesis of strong back radiation and warming of the Earth's surface, claim that not only is the surface emissivity nearly that of a black body radiator, but that 100% of any back-radiation from greenhouse gases is absorbed by the surface. In emission mode, the Earth's surface is either a black body emitter or nearly so, they say, and it is a black body absorber of the thermal infrared radiation emitted from the Earth's surface.
Real materials do not have excitable harmonic oscillator responses at all frequencies. In fact, infrared spectroscopy has long taken advantage of the discrete and characteristic absorptions that different materials have to identify those materials. We can use an infrared spectrometer to determine whether a material has water in it. We use it to distinguish polypropylene from polyethylene, polystyrene, and cellulose. It can be used to identify various sugars, starches, and proteins. Yet, the climate alarmists often claim that organic materials all behave very much like black body radiators and absorbers, emitting and absorbing radiation at all frequencies, at least all thermal infrared frequencies. Well, no they do not.
That the Earth's surface materials are not black body radiators and absorbers matters. For instance, if the emissivity is calculated which would cause the Earth with no greenhouse gases to have an average temperature of 287.64K or 14.5C with the absorbed solar insolation average power density we calculated above of 255 W/m^2, then the emissivity would be 0.657. Is this a plausible effective emissivity for the real Earth surface? And note that if the surface emissivity is less than 0.657, then there have to be other cooling mechanisms to bring down the equilibrium radiative temperature which then would be higher than 14.5C.
Let us look at a portion of the Earth's radiative output according to the IRIS satellite looking down on the dry Sahara Desert in the figure below. Note that both at the low wave number end and the high wave number end this spectrum is truncated. It is truncated at the low wave number end because most infrared spectrometers use window and other materials which absorb too much infrared radiation at lower wave numbers. There are specialized near infra-red instruments that can make measurements in that lower number range by using different materials. I do not know why this spectrum is cut-off at the larger wave number end. My infrared spectrometer acquires spectra from 400 to 7800 wave numbers. Customarily, we cut our spectra off at 4000 wave numbers, because we almost never see any absorptions in materials between 4000 and 7800 wave numbers. This figure also presents a model that calculates infrared absorption by greenhouse gases, which curve is shown in red. At the moment, we are not interested in this.
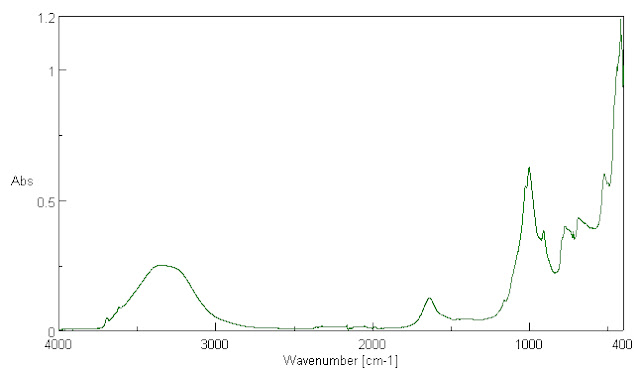
Since water covers about 70 to 71% of the Earth's surface, let us examine the infra-red absorption spectrum of water. It is presented in Fig. 3.
Let us assess this water spectrum. First, the absorption from 4000 to 7800 wave numbers was zero. Second, if we generously assume that the maximum absorption here at about 400 wave numbers is a wavelength at which water is sort of a black body absorber, then if at every other wavelength it absorbed the same amount of radiation, we might take this to indicate a material with an emissivity of 1 over these infrared wavelengths which are found in the same range as the emissions from the Earth. Note that if CO2, whose main absorption is shown in Fig. 2, were causing radiation to be emitted from it back to surface water, the water absorption spectrum does not indicate black body absorption in the vicinity of 675 wave number.
In most other parts of the water spectrum the absorption is even lower. The integrated area under the absorption curve compared to the area if absorption were everywhere from 400 to 4000 wave numbers equal to the maximum absorption is a fraction of 0.192. The settled science of the global warming community says that the emissivity is equal to the absorptivity. This is not actually true for non-black body materials, but if it were true for water, then it would be reasonable to think of this as the average emissivity over this range, and this is much smaller than 0.95.
Could it be that land material emissivities are gigantic and very black body like? The greenhouse gas proponents claim it is for organic materials, such as plant life. Let us examine a blade of green grass.
If we take the absorptivity of the green grass blade as one when the absorption across the range is equal to its maximum amount, then the ratio of the actual absorption to that is only 0.207. A green leaf from a bush is similar, though slightly more absorbing by the maximum absorption criterion without taking into account the absolute absorbance from the spectrum. The maximum peak absorbance for the bush leaf was less than that of the grass blade.
Fig. 5. The FTIR infrared spectroscopy absorption spectrum for a green leaf from a bush. As with a blade of grass, this leaf is full of water and the water peaks are all present.
Taking the ratio of the actual infrared absorption to that if there were uniform absorption at the maximum value, the absorptivity is then 0.269. This method should produce an upper bound on the absorptivity. Then if we say as the greenhouse gas advocates do that the absorptivity equals the emissivity, we have an emissivity of less than 0.269. Comparing this to the green grass blade, it is actually clear that the maximum absorption was lower for the bush leaf than for the blade of grass. It is not really significant that the ratio value calculated is larger than that for the blade of grass. What is important is that there is good reason to believe neither plant is even close to that of a black body radiator.
Is the story different for soil? The FTIR infrared absorption spectrum follows:
Fig. 6. The infrared absorption spectrum of a moist and fairly rich soil. The maximum absorption just above 400 wave number is actually very high, but the integrated absorption ratio to that of the constant absorption at the maximum rate is very low.
The soil spectrum has less water in it than the grass and bush leaf spectra showed. If we most generously take the maximum absorption to be that of a black body radiator, the actual absorption is only 0.123 of that. Again, if the emissivity were equal to this upper bound absorptivity level, than it would also be only 0.123. Again, this is far short of 0.95.
Of course soil has both inorganic minerals in it and decayed plant materials. Let us examine the infrared absorption spectrum of a feldspar mineral:
Relative to the strongest absorption peak, the absorptivity overall in this range of the infrared spectrum is about 0.117. If the emissivity were equal, it would not be greater than 0.117 also.
Finally, let us consider a common, but simple mineral, sand:
Treating the strongest peak as locally the equivalent of a black body radiator is surely wrong. Give this peak all the spinach you want and it will not become black body radiator like! This is a weakly absorbing peak. But, again being otherworldly generous, if it were the level of absorption of a black body radiator, this sand would have an absorptivity of no more than 0.098. This is about an order of magnitude lower than the Earth surface emissivity claimed by greenhouse gas supporters to be 0.95.
In another post, I found the Earth's effective surface emissivity to be between about 0.45 and 0.50. Because the absorptivity values in the infrared spectra I have given above are so low, either the emissivity values are significantly higher than the absorption values or there would appear to be a problem. Now while the emissivity values can be higher for a non-black body material, much of the explanation is found in another simple matter which has been overlooked by the incredibly well-funded settled scientists of the greenhouse gas theory.
The power density side of the Stefan-Boltzmann equation P/A = ε σ T4, uses a very simple and gross idea of area. The square meter is defined by a square with sides of 1 meter each. But when the Earth is radiating from a grassy field, the radiating surface area is not 1 square meter inside that square with sides of 1 meter length. The relevant emitting surfaces are the area of every blade of grass and any exposed soil between the blades of grass. The emitting surface area may be 2 or 2.5 times the nominal area of 1 square meter of ground. Even the sandy beach will have the surface area given by following the surface area of every grain of sand. Surely there is emission from the ground under the tree, the trunk, the branches, and the leaves in many land areas. Even the oceans will have maybe 1.2 times the emitting surface area of the nominal square which is used on the power side of the radiation equation due to waves and ripples.
The energy the surface absorbs from the sun is distributed to some depth in the oceans or into the soil or rock surface on land. The heat absorbed on average each day is far more reasonably provided by the simple 1 meter by 1 meter average power density provided by the sun. But that energy is then also supplied to each bit of infrared radiation emitting surface area as the emission depletes the stored energy in the surface and the near surface. Thus, effectively, the area on the right side of this Stefan-Boltzmann equation representing surface emission is almost always larger than the area on the left side taken to represent the area of solar insolation absorption. Most surfaces on the Earth surface will definitely have a larger emitting surface area. This has the effect of multiplying the emissivity of the emitting material by the ratio of the greater surface area emitting. The ratio of the emitting surface area to the solar radiation area is multiplied times the normal laboratory measured emissivity of the emitting material. The increase in the effective emissivity of the Earth surface is substantial.
Now note that the greenhouse gas claim that infrared absorbing gases cause a very large increase in the Earth's surface temperature is based on a claim that the emissivity of water and plants is 0.95 or even 1.0. If this were so, then this observation of the need to account for the greater emitting surface area would create a whole different problem for their theory. What they claim is a measured 0.95 emissivity for water would become a super black body emitter with an effective emissivity of say (1.2)(0.95) = 1.14 due to the waves of the ocean increasing its emitting surface area. The situation over the prescribed grassy field for land surface temperature measurements would be even worse. One might easily have an emitting area two times the nominal square area, so the grassy surface emissivity would be 2 (0.95) = 1.9. Imagine all of that radiation converging on their temperature station only 1.5 meters above this super, super black body radiator!
This conclusively demonstrates that it is very plausible based on laboratory spectra on the materials from the surface of the Earth that the effective emissivity of the surface of the Earth is less than 0.5. Any effective Earth surface emissivity less than 0.657 as I showed means that there is no warming effect due to the so-called greenhouse gases. Indeed, an effective Earth surface emissivity of less than 0.5 is consistent with a net cooling effect due to the infrared active gases of water vapor, carbon dioxide, methane, and nitrous oxide. I have stated elsewhere why this is what we should expect. I will write more about this in the near future.
Posts
No comments:
Post a Comment