This article explains the basic physics relevant to the Catastrophic Man-Made Global Warming hypothesis. It provides the background needed to see why the hypothesis is wrong. Of course, it has to be wrong because the empirical test of the predictions of the climate models based on their claimed version of the physics has shown those models to fail for 18 years now. It was always a farce to call the science settled in any case, since the models supposedly based on the settled science show the science is highly unsettled by their wide divergences in the predictions they make, despite their general bias on the scientific inputs and modelling methods towards a false warming caused by so-called greenhouse gases.
Infrared-Absorbing Gases and
the Earth's Surface Temperature:
A
Relatively Simple Baseline Evaluation of the Physics
Charles
R. Anderson, Ph.D., Physics
Introduction
This analysis of the Earth’s surface temperature will examine the case of an Earth in radiative equilibrium with space, assuming a constant solar insolation as the critical radiative source of energy. It will evaluate the role of the so-called greenhouse gases, which are really infrared absorbing and emitting gases, in our atmosphere in establishing the surface temperature of the Earth. The emphasis will be on examining these long-term baseline equilibrium effects. Clearly the sun has solar cycles, cooling cloud cover varies greatly, and the oceans with their huge heat content and slow response times to changes in solar insolation have their cycles also. These are terribly important effects, but they are not primary to the evaluation of the claim that increases in carbon dioxide in the atmosphere will lead to a catastrophic global warming. The examination of the basic physics undertaken here will provide a baseline understanding in terms of relatively simple physics of the role and effects of infrared absorbing and emitting gases generally within a dense atmosphere almost entirely composed of infrared-inactive gases. This paper will point out that the Earth’s surface is not in radiative equilibrium with space, though the Earth as a whole is. The fact that the atmosphere is dense, composed almost entirely of IR-inactive gases, and the role of water are the key facts in understanding the basic physics that determines the surface temperature of the Earth.
This analysis of the Earth’s surface temperature will examine the case of an Earth in radiative equilibrium with space, assuming a constant solar insolation as the critical radiative source of energy. It will evaluate the role of the so-called greenhouse gases, which are really infrared absorbing and emitting gases, in our atmosphere in establishing the surface temperature of the Earth. The emphasis will be on examining these long-term baseline equilibrium effects. Clearly the sun has solar cycles, cooling cloud cover varies greatly, and the oceans with their huge heat content and slow response times to changes in solar insolation have their cycles also. These are terribly important effects, but they are not primary to the evaluation of the claim that increases in carbon dioxide in the atmosphere will lead to a catastrophic global warming. The examination of the basic physics undertaken here will provide a baseline understanding in terms of relatively simple physics of the role and effects of infrared absorbing and emitting gases generally within a dense atmosphere almost entirely composed of infrared-inactive gases. This paper will point out that the Earth’s surface is not in radiative equilibrium with space, though the Earth as a whole is. The fact that the atmosphere is dense, composed almost entirely of IR-inactive gases, and the role of water are the key facts in understanding the basic physics that determines the surface temperature of the Earth.
Unfortunately, even at this baseline level of understanding, the usual explanations of the basic physics as rendered in the popular science media, government websites and publications, most newspapers and magazines, TV, many global warming alarmist websites, most high school science classes, most college courses, and even advocated by many scientific professional societies are terribly wrong. The understanding here will make it clear that it is unlikely that higher concentrations of carbon dioxide will have catastrophic effects due to significant warming of the Earth’s surface. This baseline understanding will make it clear that the advocates of such a hypothesis have failed to prove that very dubious hypothesis with its critically important implications for our daily lives, both in terms of our freedoms and our standard of living.
It is claimed by the catastrophic man-made global warming advocates that infrared (IR) absorbing water vapor, carbon dioxide, and methane gas, misleadingly called greenhouse gases, are responsible for greatly warming the surface of the Earth. Measurements of radiation power from the Earth, which include radiation from the Earth’s surface and the atmosphere with their respective temperatures and reflected solar radiation in the same frequency ranges are commonly associated with a black body radiator that would produce the same radiative power. From such a calculation, as seen from space, the Earth has an effective “black body” radiation temperature of about 255 Kelvin, abbreviated as 255K or -18ºC. The actual radiation spectrum from Earth into space does not look like the spectrum of a black body radiator at the temperature of 255K. The altitude in the U.S. Standard Atmosphere Table of 1976 with a temperature of 255K is 5100 meters. The Earth’s surface has an average temperature commonly said to be about 287.65K or 14.5ºC. The difference in these temperatures of about 32.65K or 32.65º C is very commonly attributed to the so-called greenhouse gas effect. When this difference is assumed to be due to the greenhouse warming effect, it is a big effect.
This paper will show that the Earth’s surface temperature would be much warmer than 255K in any case given that the Earth’s surface is not actually a black body radiator and is not in radiative equilibrium with space. The substantial temperature gradient in the lower atmosphere due to gravity will be calculated and discussed. It will note that the huge heat capacity of the oceans, the land surface, the subsurface materials, and the atmosphere itself is another warming effect over the daily cycle due to the effective reduction of infrared (IR) radiative cooling of the Earth’s surface averaged over the daily cycle. The combination of the gravitational temperature gradient of the lower atmosphere due to the combination of IR-absorbing and emitting gases and the density of the atmosphere provided by IR-inactive gases provides a large warming effect upon the Earth’s surface compared to the supposed 32.65K discrepancy with the Earth’s radiative temperature as seen from space.
IR-absorbing gases play a significant role in determining the surface temperature of the Earth and in the distribution of heat within the atmosphere. But, this role is almost entirely due to water vapor in the lowest part of the atmosphere, the troposphere. This role of water vapor only exists because Earth is a water-covered planet. Water also plays a critical role in cooling and moderating the temperature of the surface of the Earth by evaporation and sublimation, by lightening the air to increase convection, by increasing the specific heat of the air, by forming clouds, and by condensing in clouds to form ice and water droplets with the release of great quantities of heat, which causes cloud expansion with further cooling of an enlarged shadowed surface area. Water vapor and carbon dioxide also have underrated roles in absorbing solar insolation in the atmosphere and preventing solar incoming IR radiation from warming the surface to what actually might be catastrophically high temperatures.
The natural effects of liquid water and water vapor dwarf the effect of further additions by man to the rare IR-absorbing gases of CO2, methane (CH4), and nitrous oxide (N2O). I will provide reasons why these rare IR-absorbing gases are much less effective in providing back-emitted IR radiation originally from the surface which the surface can absorb than is water vapor. I will also point out why water vapor is itself less effective in warming the surface by re-emitted IR radiation it has absorbed from surface IR emission than is usually thought to be the case by the catastrophic man-made global warming advocates. The effect of IR radiation from the atmosphere upon the surface temperature has been generally greatly over-estimated while the size of the natural effects of the previous paragraph has been greatly underestimated.
I will show that the essential physics can be summarized as:
- Infra-red active (so-called greenhouse) gases absorb a substantial portion of the incoming solar radiation in the infrared portion of its spectrum with the result that additions to their concentrations have a cooling effect.
- The Earth's surface is not a black body radiator, so it takes much less absorbed solar radiation to warm it to 287.65K or 14.5ºC than the alarmist greenhouse gas theories claim. In fact, the Earth's surface is only about half as efficient an infrared radiator as is a black body.
- The Stefan-Boltzmann law of radiation applies to a surface radiating into vacuum, not into an atmosphere able to provide competing cooling processes due to air conduction, air convection, and water evaporation. This Stefan-Boltzmann radiation equation provides the total cooling power from a surface at a given temperature. This will all be in the form of radiation in the case of the surface interfaced to vacuum. Due to energy conservation, the radiation resulting when interfaced to an atmosphere will be that total power minus all of the cooling by other competing cooling mechanisms. The alarmists add the other cooling mechanism's power to that of a 100% efficient black body radiator. They then seek a convoluted reason to provide more counteracting warming to this excessive surface cooling in the form of a massive back-radiation.
- At the Earth's surface, the sum of evaporative, conductive, and convective cooling exceed radiative cooling, contrary to the usual alarmist theory.
- A short distance of 100 or 200 meters above the surface, the 65% of the surface infrared radiation that can be absorbed by IR-active gases has been absorbed already due to short mean free path lengths and the energy has been distributed to the non-radiating molecules of the atmosphere due to extremely high collision rates. Only the 35% of surface radiation into the atmospheric window continues on into space under rapid radiative transport. This is 35% of a much smaller amount of surface radiation than posited by the alarmist theory.
- The temperature gradient in the atmosphere near the surface is mostly characterized by slow energy transport mechanisms, not by extremely fast radiative cooling mechanisms imagined by the alarmist theory. Energy transport here is almost entirely upward. Radiation transport is just in very short hops between layers of air usually differing very little in temperature and with few molecules capable of radiating infra-red radiation. This lower part of the troposphere is critically and fortunately not in radiative equilibrium with space.
- Most of the radiation into space is from the upper zone of substantial water vapor concentrations or from still higher altitudes by carbon dioxide. The difference is radiation from the surface into the atmospheric window. The effective temperature of the Earth system as a unitary radiator seen from space is 255K, although only in that it would generate the right amount of total energy as a black body radiator. This temperature is such that it balances the Earth's total absorbed radiation from the sun with an equal cooling radiation into space. This effective black body radiator temperature has no simple connection with the Earth's surface temperature which is the temperature of most importance to human life.
- The gravitational field of the Earth and the Conservation of Energy for static air produce a temperature gradient in the lower atmosphere, the troposphere, which is linear with altitude. In the lowest 5000 m, this decreasing temperature gradient with increasing altitude is about 6.5K/km for dry air. The altitude of effective radiative equilibrium with space at a temperature of 255K is about 5100 meters. Starting from there with a gradient of 6.5K/km produces a temperature at the bottom of the atmosphere of 288K. This matches the average surface temperature.
- The lower atmosphere always has some rising, non-static air due to convection. This rising air expands due to the dropping pressure and cools as it does so. Depending upon the amount of rising convection, the temperature gradient in the troposphere may become as large as 9.78K/km in the bottom 5 km of the atmosphere. The gradient will then be between 6.49 and 9.78K/km depending on the amount of upward air convection. This applies unless winds carry air from areas receiving very different amounts of solar insolation to disturb the area.
- Added carbon dioxide in the alarmist theory causes an increase in back radiation, or in radiation from the Earth's surface being returned to it. But the alarmists overstate the radiation emitted from the Earth's surface by a factor of two and they overstate the radiation returned to the Earth's surface hugely.
- The limited radiation from the Earth's surface that can be absorbed by carbon dioxide is almost entirely absorbed within 100 or 200 meters from the surface. The heat transported by radiation is quickly spread to non-radiating nitrogen and oxygen molecules and to argon atoms that make up 99.97% of the air due to the 6.9 billion collisions per second of molecules. This adds to the slow convective transfer of heat upward.
- Carbon dioxide molecules in the air are rare and will radiate infrared radiation, but it will be at the energy level of the temperature of the surrounding air molecules. Thus they radiate toward the surface as cooler molecules and upward as warmer molecules relative to potential absorbers given the normal temperature gradient in the air with altitude. Consequently, carbon dioxide emitted radiation speeds the transfer of heat toward higher altitudes slightly and only under relatively infrequent conditions can supply the surface with added heat. Carbon dioxide is only about 0.04% of the molecules in the air, placing a limit on the amount of heat transfer at particular wavelengths by so few molecules.
- When the relatively infrequent conditions exist that the emitting carbon dioxide molecules in the air above the surface are warmer than the surface, carbon dioxide emitted radiation is less effectively absorbed by the surface than is that from water vapor. This is because some of the characteristic radiation frequencies of carbon dioxide are not as likely absorbed by water that covers 71% of the planet or by plants based on a water-rich chemistry or by soils and minerals with their commonly high water content.
- Incoming solar radiation is about 49% infrared. Some of this is absorbed in the atmosphere by added carbon dioxide before it can reach the surface and warm it. This results in a cooler surface.
- Carbon dioxide mostly emits radiation into space from altitudes exceeding 9 km and extending to 20 km. From 11 to 20 km there is no temperature change, there being a uniform temperature of about 217K, at least in the U.S. Standard Atmosphere. There may be some temperature change in a tropical atmosphere. There is a version of the carbon dioxide warming theory that more carbon dioxide emitters at this altitude decrease the cooling efficiency of the Earth and that warms the atmosphere below it. Adding carbon dioxide at these altitudes does much less to change the temperature of the emitting molecules since they are already largely emitting in the constant 217K zone. What is more, fast radiative cooling has already become the almost exclusive mode of moving heat to higher altitude and to space due to the water-rich radiation zone at much lower altitudes. More carbon dioxide absorbers at a higher altitude just simply re-emit the radiation quickly into space due to the low gas molecule collision rates. Any radiation directed downward is quickly turned around and also sent into space.
- Even with the considerable very bad physics used to justify a warming effect by carbon dioxide, the warming effect wrongly claimed by the IPCC was only 1.2K upon doubling the amount of carbon dioxide. They then invoked a claimed stronger reinforcing warming due to increased water vapor to make a total warming of 5.4K. Experimental measurements, eons of relatively stable climate, and the expectation of additional cloud cooling and additional solar radiation absorption in the atmosphere due to added water vapor all indicate that increased water vapor would actually provide a negative feedback or a counteracting cooling effect even it added CO2 were to produce a slight warming. Actually, additional CO2 would produce a slight cooling effect.
- The health of plants, upon which we humans and other animals are so dependent, is improved with higher concentrations of carbon dioxide. Carbon dioxide is essential plant food. The improved growth of plants uses up a good portion of any additional carbon dioxide added to the atmosphere.
- Increased infrared active gases tend to moderate the temperature variations of night and day. This is a good thing.
Greenhouse Gas Hypotheses
The physics offered in support of the hypothesis that IR-absorbing gases are responsible for the large 32.65ºC temperature difference between the Earth’s calculated effective “black body” temperature of 255.0K and the average sea level surface temperature of about 287.65K has some big obstacles to overcome. Proponents of the hypothesis claim that solar radiation is transmitted through our atmosphere in the short wavelength portions of the electromagnetic spectrum as ultra-violet, visible light, and the relatively short wavelength portion of the infrared radiation dominant in the solar spectrum with little absorption. This radiation is absorbed by the surface of the Earth and warms it.
The Earth’s surface then emits
long wavelength infrared radiation upward into the atmosphere. The infrared absorbing gases in the
atmosphere absorb most of the IR radiation and re-emit half of it into space and half
of it back toward the surface of the Earth. For this to be true without substantial
energy losses, the time for re-emission of the energy of the absorbed photon
must be very short compared to the time between gas molecule collisions, or some
of the energy will be transferred to other IR-inactive gas molecules. In
addition the mean free path for absorption of an IR-emitter photon before it is
absorbed by an IR-absorber molecule must be large.
Proponents of the catastrophic greenhouse gas hypothesis commonly then claim that the half re-emitted back to the Earth’s surface is then absorbed by the surface and re-emitted toward the atmosphere. A second time the IR-absorbing gases absorb this IR radiation and half of the half is emitted again toward the Earth’s surface. This process repeats infinitely and the net result of adding up all the halves of halves of halves, etc., in a geometric series is said to be about a doubling of the warming power of the solar radiation initially incident upon the surface in the form of back-emitted radiation. Well, this is an interesting violation of energy conservation, so it does not happen. What is more, they assume that the Earth’s surface absorbs all of this re-emitted and returned radiation.
Proponents of the catastrophic greenhouse gas hypothesis commonly then claim that the half re-emitted back to the Earth’s surface is then absorbed by the surface and re-emitted toward the atmosphere. A second time the IR-absorbing gases absorb this IR radiation and half of the half is emitted again toward the Earth’s surface. This process repeats infinitely and the net result of adding up all the halves of halves of halves, etc., in a geometric series is said to be about a doubling of the warming power of the solar radiation initially incident upon the surface in the form of back-emitted radiation. Well, this is an interesting violation of energy conservation, so it does not happen. What is more, they assume that the Earth’s surface absorbs all of this re-emitted and returned radiation.
There is a second, less common, version of the greenhouse gas warming of the Earth. It basically says that greenhouse gases at substantial altitudes cool the Earth by radiating energy off into space. The argument then says that adding more of an IR-absorbing and emitting gas at higher altitudes in the atmosphere will cause more of the IR-emission to be from cooler molecules as they absorb energy emitted by IR-active molecules at lower altitudes. They then must disperse some of that energy to the IR-inactive molecules around them, though this is less likely at these higher altitudes with reduced pressure than it was at lower altitudes. They claim this decreased cooling at high altitudes causes the lower altitudes and the surface of the Earth to warm. This argument is often brought forward when the usual high surface emission and high surface absorption of a very high back radiation argument is defeated. The reader might want to think about the inconsistency of this high altitude argument with assumptions made in the back radiation argument. We will talk about this argument late in this paper as well as another high altitude argument which is totally inconsistent with this version of the high altitude radiation argument.
IR-Active or Greenhouse Gases
All IR-absorbing gases do is capture energy for an instant due to the vibrational excitation of their chemical bonds or due to inducing electronic transitions and then they release it, either by radiating it away or by colliding with another gas molecule such as the predominant nitrogen or oxygen molecules and transferring energy to them. These predominant molecules of nitrogen and oxygen then transfer this collision-absorbed energy through convection and gas collisions with other molecules. But, none of these effects do more than transfer energy. They do not create it. They do not magnify the energy of the sun or serve as a supplementary source of energy, though the evaporation and condensation of water do greatly affect the distribution of energy in the atmosphere. There is no analog to these many water vapor roles for the much rarer CO2, methane, or nitrous oxide. In addition, the lifetime of methane and nitrous oxide is shorter since they are broken down by UV radiation.
Another basic reason the greenhouse gas or IR-absorbing gas idea of emitted, half re-absorbed, and then re-emitted, then half re-absorbed once again in a geometric power series does not work is because the photons of radiation inside a black body radiator do not behave like ordinary particles. They are bosons and radiation from the walls of the black body varies to keep the conditions on the hollow interior of a black body sphere at constant temperature in equilibrium. The energy density per unit interior volume remains constant for a given temperature inside the black body sphere even if you expand the sphere and make it bigger. To keep that constant energy density per unit volume, the walls actually produce more photons per unit area when you make the sphere volume larger. This larger flux of photons off both the inner wall and outer wall surfaces corresponds to the same black body temperature. Doubling the radius of the black body sphere of a given temperature causes the flux of photons per unit surface area to also double. This is not very intuitive for most people. Indeed, it is not intuitive to most people who have long studied physics. You cannot in a similar way increase the number of atoms, for instance.
The chemical potential of black-body radiation is zero, which is a most remarkable property. This can contribute to many misunderstandings of how black body radiation is to be applied to real-world objects. It also is important in understanding why a warmer body does not generally absorb radiation from a cooler body, despite a flux of photons from the cooler body being incident upon the warmer body. Due to local fluctuations and to the Boltzmann velocity distribution of gas molecules there are some exceptions of absorption in the Earth's surface of a photon emitted from somewhat cooler air above it, but this is a very insignificant effect.
The chemical potential of zero also causes problems with even thinking you can follow the emissions of individual photons and count them and figure out how many are absorbed by IR-absorbing gases and then how many photons are emitted by the excited gas as radiation versus how much of the energy absorbed by the IR-absorbing gas is lost due to collisions with the many other gas molecules in the lower atmosphere. This is a real problem, since below about 4000 meters altitude, more energy is transferred by collisions, mostly to nitrogen and oxygen molecules, than is transferred by radiation. To further complicate things, energy is also transported by the evaporation of water, the sublimation of ice, the condensation of water vapor, by air conduction and convection currents, by winds, and by the expansion of warm air as it rises. These other energy transfer mechanisms are the reason why the Earth’s surface itself is not in thermal radiative equilibrium with space as the sphere at the 5,100 meter altitude effectively is.
Heat Capacity of the Surface Effects
A very
interesting article by Martin Hertzberg, Hans Schreuder, and Alan Siddons
called A Greenhouse Effect on the Moon?, should be summarized here and
discussed in this context. The moon has
no atmosphere and it is the same distance from the sun as the Earth is. Yet, the mid-day temperature on the moon's
surface is about 370K or about 97º C, which is about 20K cooler than expected
just due to the radiation incident from the sun. The nighttime temperature gets down to about
85K or about -188º C, but this is about 60K warmer than the expected low
temperature due to radiative cooling as the only nighttime energy flow. See the daily temperature profile in the
figure below comparing the predicted temperature with the actual
temperature.
The reason for the difference is that the surface of the moon holds and retains heat into its night due to its heat capacity and the sub-surface remains somewhat cooler than the immediate surface during its day. The subsurface rock cools the surface then. These effects make the average temperature of the moon’s surface about 228K. This is about 40K warmer than it would otherwise be due to reduced radiative cooling during the day and increased radiative cooling during the night. The night cooling is at a much less cooling-efficient lower temperature than the day temperature. This increase of average temperature over the daily cycle owes to the fourth power dependence of radiative cooling on the temperature and the large daily swing in the temperature.
The reason for the difference is that the surface of the moon holds and retains heat into its night due to its heat capacity and the sub-surface remains somewhat cooler than the immediate surface during its day. The subsurface rock cools the surface then. These effects make the average temperature of the moon’s surface about 228K. This is about 40K warmer than it would otherwise be due to reduced radiative cooling during the day and increased radiative cooling during the night. The night cooling is at a much less cooling-efficient lower temperature than the day temperature. This increase of average temperature over the daily cycle owes to the fourth power dependence of radiative cooling on the temperature and the large daily swing in the temperature.
Fig. 1. The predicted temperature of the moon’s
surface with no ground thermal conductivity and sub-surface heat capacity
compared to the real measured temperatures. The blue line shows the expected
temperature if the subsurface heat capacity did not play the moderating role it
does.
Analogously, the Earth's land surface, its oceans covering 70% of the planet, and its atmosphere all have a heat capacity and provide for a substantial flow of heat to the surface from their interiors at various times of the day. The heat capacities of the Earth’s surface and atmosphere greatly exceed that of the rock of the moon, especially thanks to our oceans, so the day to night moderating effect seen on the Earth is much larger than it is for the moon. It is true, as pointed out by Rosco in a comment, that the moon also achieves both higher and lower temperatures than would the Earth simply because its daily cycle is much longer. Nonetheless, the radiative equivalent temperature of the Earth as a whole and averaged over the day would be lower than 255K if the solar insolation reaching the surface were unchanged because higher daylight temperatures would cause more effective cooling during the day than during the night.
The size of the effect of the ocean is found to be most dramatic for small islands surrounded by ocean in the equatorial area in which the day to night temperature shift is very small. This much more moderate difference in the day and night surface temperatures results in a much lower effective increase in the surface temperature than the 40K increase seen on the moon due to differences in the radiative cooling between day and night.
But with the fairly typical 22ºF high to low temperature difference at the mid-latitude Baltimore-Washington International Airport averaged over a year, the radiative cooling at the daily high temperature is about 18.5% more efficient than the radiative cooling at the daily low temperature. We also have to remember that like the moon, we have an underlying warming effect due to the sub-surface storage of energy at night and the cooler sub-surface during the day. The extreme moderation of the Earth’s daily cycle is also the only reason we can even do baseline calculations at all using a daily average set of conditions without huge errors. We should remember that this is still a crude approximation and that we are making it still cruder by ignoring the wider differences in radiative cooling between the Equator and the Poles.
The Black Body and the Earth Radiator
Let us examine some of the properties of black body radiation for a moment. The power in Watts (W) radiated by a black body surface at a temperature T (in Kelvin) into vacuum is given by the Stefan-Boltzmann Law formula:
P
= A ε σ T4,
in which A is
the radiating area in square meters, σ = 5.6697 x 10-8 W/m2K4
the Stefan-Boltzmann constant, and ε = 1.
A watt is equal to a joule/second, or J/s, and a joule is a unit of energy. Heat is energy.
The area of a sphere of radius r is 4 π r2. The altitude of 5000 meters above sea level according to the temperatures of the U.S. Standard Atmosphere of 1976 is 255.7 K, which is almost equal to the Earth’s effective black body radiation temperature as seen from space, which is about 255K. The altitude actually at 255K is about 5105 m. By this it is only meant that a black body radiator at the temperature of 255K would radiate the same total amount of energy as the Earth does. The Earth’s radius is about 6,376,000 meters, so the effective sphere that is in equivalent radiant equilibrium with space has a radius slightly larger of about 6,381,100 meters. If this sphere’s surface were uniformly at the temperature of 255K, then its total radiant outward power would be 1.227 x 1017 W. That sphere would also emit a total inward radiant power of the same amount and all inside the shell wall of the sphere would be in equilibrium, were it not for our atmosphere.
The area of a sphere of radius r is 4 π r2. The altitude of 5000 meters above sea level according to the temperatures of the U.S. Standard Atmosphere of 1976 is 255.7 K, which is almost equal to the Earth’s effective black body radiation temperature as seen from space, which is about 255K. The altitude actually at 255K is about 5105 m. By this it is only meant that a black body radiator at the temperature of 255K would radiate the same total amount of energy as the Earth does. The Earth’s radius is about 6,376,000 meters, so the effective sphere that is in equivalent radiant equilibrium with space has a radius slightly larger of about 6,381,100 meters. If this sphere’s surface were uniformly at the temperature of 255K, then its total radiant outward power would be 1.227 x 1017 W. That sphere would also emit a total inward radiant power of the same amount and all inside the shell wall of the sphere would be in equilibrium, were it not for our atmosphere.
If we assume that the sphere with the temperature of 255K is in equilibrium with a slightly smaller black body sphere of the radius of the Earth at sea level, we can calculate the temperature of that surface given that it must radiate a power equal to the power of the surrounding sphere which is in equilibrium with space. The temperature will be higher, since the surface area of the sphere is smaller. In fact, the temperature of the Earth’s surface as a black body would be 255.100K or 0.1ºC warmer than the sphere at the altitude of 5100 meters above sea level which is in equilibrium with space in this very simple model. Thus we see that the altitude itself of the radiating surface, whether the Earth’s surface or the weighted average altitude in the atmosphere makes no significant difference from the standpoint of the size of the radiating surface.
But the Earth is not really a black body, so the Stefan-Boltzmann equation has to have an emissivity factor, ԑ, multiplied times the temperature side of the equation. For the Earth as a whole, this emissivity factor is often said to be about 0.7. This is an effective emissivity of the Earth’s surface and the various altitudes of its atmosphere combined in some unknown weighted average. This causes the Earth’s effective radiative altitude or plane to have to be at the more elevated temperature of 278.9K to be in equilibrium. This effective sphere with this temperature is somewhere between the Earth's surface and altitudes from which most atmospheric radiation into space occurs. The effective plane of radiation according to the U.S. Standard Atmosphere with this temperature is at 1433 m altitude. Thus it is reasonable that the temperature we calculate here is between that of the surface and the cooler altitude from which much of the atmospheric radiation is emitted. This plane is only about 8.75K or 8.75ºC below the surface temperature of 287.65K. Thus, the effective radiative plane temperature differs from the surface temperature by only 26.8% of the 32.65K claimed greenhouse gas contribution. The surface temperature is warmer than this, as it should be, and there is no great temperature discrepancy to be explained.
Of course, the sphere around the Earth with a radius 5,100 meters greater than that of sea level is not really at a constant temperature, since part of the Earth is in daylight and part is in nighttime. Nonetheless, the above calculation gives us a good sense of the magnitude of real radiant effects by black body (ε=1) and gray body (ε less than 1) radiators because for Earth the day and night temperatures are not terribly different, given the wondrous effect of its very high heat capacity near the surface. The gray body calculation makes it very clear that any IR-absorbing gas effects that do exist do not necessarily provide a 32.65º C increase of the surface temperature in the way in which that is usually described by alarmist propaganda.
The widely used 1997 version of the Kiehl-Trenberth energy budget for the Earth is given in Fig. 2 below. This energy budget was featured in the UN IPCC 4th report of 2007. The right-hand side and center of this diagram showing surface cooling effects and back-radiation is total nonsense, while the left side showing solar insolation and the effects upon it, is not so far from the truth. According to this diagram, about 198 W/m2 of solar insolation reaches the surface, but about 15.2% of that is reflected. It is probably more realistic that 64% of the solar insolation is incident upon the surface, which is 219 W/m2, and if 15.2% of that is reflected, then the surface absorbs about 186 W/m2 with about 33 W/m2 reflected from the surface. The radiative cooling potential of a surface into vacuum absorbing an influx of power of 186 W/m2 at a temperature of 14.5ºC, or 287.65K, implies that
P = 186 W/m2 = ԑ σ T4 = ԑ (5.6697 x 10-8 W/m2K4)(287.65 K)4,
Where ԑ is the emissivity of the Earth’s surface, which implies ԑ = 0.479.
Performing the same calculation using the K-T diagram absorbed solar insolation at the Earth's surface yields a lower bound emissivity of 0.433. This is the lower bound because it assumes that the solar insolation absorbed by the atmosphere is not re-radiated to the Earth's surface and absorbed there. Actually, it is not really even a lower bound effectively because we are also assuming here that the Earth's surface has no other mechanisms for losing heat. We are explicitly ignoring the evaporation of water, conduction, and convection currents!
We can obtain an upper bound emissivity for the Earth's surface as well. Let us be very generous and assume that half of the incoming solar flux absorbed by the atmosphere is re-emitted toward the surface and half toward space. The highest energy flux that could be absorbed by the surface would then be the direct 168 W/m2 directly absorbed according to K-T and half of the 67 W/m2 they claim was initially absorbed by the atmosphere. This very generous upper bound of 201.5 W/m2 would mean that the emissivity into space was 0.519. Note that this is the emissivity of the surface of the Earth, which is different from the weighted average of the Earth’s surface and the atmosphere at altitude in radiative equilibrium with space, which we said earlier had an effective ε about 0.7.
So, the K-T diagram implies that the Earth's surface emissivity lies between about 0.43 and 0.52 if the Earth's surface were in equilibrium with vacuum. The source of energy flux into the Earth's surface is the energy from the sun, ignoring the very minor contribution from the Earth's hot interior. So, if the Earth's surface interfaced to vacuum, it would have to have an emissivity of about 0.48 to equilibrate the energy flux into the surface with that emitted from it at a temperature of 287.65K. But because other energy transport mechanisms are at work at the interface, the equation will only provide us with the total energy transported across the interface. That energy will now be such that the sum of all such energy transport fluxes will equal about 186 W/m2 to use my preferred value between the direct solar insolation of 168 W/m2 and the upper bound of maximum solar power possible obtained by adding in half the solar insolation absorbed by the atmosphere giving 201.5 W/m2. The emissivity is then about 0.48, which hugely bothers the many climate scientists who claim the emissivity is about 0.95 or maybe 0.93. For further insight into the reasons for such a reduced effective emissivity see my post The Greenhouse Gas Hypothesis and Thermal Radiation -- A Critical Review.
There is no way to conserve the input energy from the sun and arrive at an effective surface emissivity for the Earth's surface of 0.95. Near the end of this paper, I will present many infra-red absorption spectra of common materials found at the Earth's surface and it will be readily observable that the absorptivity is not close to 0.95 for any of the materials. This makes it very unlikely that their emissivity is close to 0.95 either.
There is still another way in which the emissivity here is an effective value. While the temperature we associate with the surface is 287.65K, the very thin layer of the last few nanometers of material before the interface with the air is cooler due to water evaporation from that surface and through much of the day due to cooler air molecule collisions with the surface. Thus the surface emission radiation is actually going to be suppressed by this cooler temperature immediately at the surface due to limited thermal conduction of materials, but the total energy transport across this thin layer must be the same whether the atmosphere causes this or not. When using the supposed warmer temperature of that surface, one winds up compensating by calculating too low an emissivity. Consequently, this calculated Earth emissivity above is an effective emissivity.
It is not surprising that it is lower than the 0.95 to 0.98 emissivity claimed for water in the mid-IR wavelengths. Those water emissivity measurements are very hard to make and may be unreliable in any case. It is clear that water is not a black body like absorber of IR radiation as we will see later. That being the case, it is surprising that it is claimed to be a near black body emitter. According to Kirchoff's Law, the emissivity and the absorptivity are equal under equilibrium radiative conditions. In truth, they need not be equal for gray body radiators. What is more, as shown in my post The Greenhouse Gas Hypothesis and Thermal Radiation -- A Critical Review, emissivity and absorptivity often cannot be equal even in steady state conditions when heat is radiated from a warmer body to a cooler body or when one body is undergoing a temperature change. Water is actually relatively transparent to infra-red at many wavelengths, though the absorption, as seen later in Fig. 7. is never zero below 3700 cm-1, so complete absorption may take many meters of depth below the surface. Most of the Earth's surface is covered with highly impure ocean water with many particulates suspended in it and these are scatterers that may scatter infra-red radiation back to the atmosphere.
More important, the solar insolation absorbed a meter below the surface is absorbed into a layer of water that is cooler than the air an equal distance or even several times the distance above the water. This means that there is no radiative transfer of heat from that cooler water layer to the air above the water. Now for those infra-red frequencies where the emissivity of water is high, water vapor above the surface of the water can absorb the emitted infra-red, provided that the water vapor absorber is at a lower temperature than the water molecule at a depth below the surface. But the common mean free path for water absorption is so short in the several meters above water surfaces at these frequencies that this condition is not often met. On the other hand, liquid water will emit at frequencies which water vapor cannot absorb, so the lower probability emission events at these frequencies can travel through the atmospheric window and so a low level of radiation from beneath the surface layer of water may occur. The end result is that despite the apparent high absorptivity of the water due to the great absorption depth of most bodies of water, the effective emissivity is much lower than the apparent total absorptivity.
A reasonable estimate of the potential surface emissivity is then ԑ = 0.5. I am using the “potential” qualifier, because any other cooling mechanism reduces this radiative cooling. Therefore, this is really an upper bound on the effective ε value and the radiative cooling.
Fig.
2. Kiehl-Trenberth energy budget for the Earth of 1997. This
represents a common viewpoint of the physics that is used to justify the
catastrophic man-made global warming hypothesis. It is apparently the
settled science. It will be demonstrated to be very wrongheaded. I have
added the percentage power flux values with 342 W/m2 equal to 100% and approximately equal to one-quarter of the solar power incident upon the Earth most directly facing the Sun.
Let us use the calculated Earth surface emissivity of 0.5 then to calculate the upper limit on the surface radiation for comparison to the Kiehl-Trenberth diagram where it is said to be 390 W/m2, a power flux even larger than the 342 W/m2 incident at the top of the atmosphere as an average over the daily cycle. What we find is that the surface emits no more than 195 W/m2, which is half of the Kiehl-Trenberth surface radiation since they assumed ԑ = 1. Let me repeat that this is an upper bound. The actual radiative cooling of the surface is much less due to heat loss by air conduction, air convection, and water evaporation and other cooling mechanisms.
Discussion of the Energy Balance in the Kiehl-Trenberth Energy Budget
The consequences of this are huge. Because the catastrophic man-made global warming theory posits a huge radiative cooling of the surface due to a large radiative power flux back to the atmosphere, it is forced to conjure up some mechanism whereby a very large fraction of this power can be returned to the surface. Their large value of back radiation is 324 W/m2, which is 83% of the radiative cooling of a black body surface due to its being at the temperature of 288K! Yet each time a greenhouse gas absorbs radiation in a limited frequency range in which it can do so, it sends half the power off toward space and cannot return more than the other half toward the surface! Let us assume that half of all the power inputs into the atmosphere in their diagram are returned as absorbed IR radiation to the ground. The maximum value of back radiation would then be (0.5) (350 + 67 + 24 + 78) = 260 W/m2, not 324 W/m2. Yet even this is too high to be a proper upper limit, since the potential ground radiated power is only about 195 W/m2.
There is another problem here as well. If half of the radiation in the atmosphere is returned to the surface and half is emitted into space and they claim that 324 W/m2 is returned to the surface, where is the 324 W/m2 which is emitted into space? In fact one should have the 40 W/m2 emitted from the surface through the atmospheric window without absorption added to the supposed 324 W/m2 emitted from the atmosphere after being absorbed there and to the 30 W/m2 which appears to be due to the heat of condensation of water in clouds causing cloud tops to emit IR into space. The sum of these quantities would be 394 W/m2. This greatly exceeds the original incoming insolation of 342 W/m2 minus the reflected portion of that which is 107 W/m2, for a remainder of only 235 W/m2.
The energy flux into space should be 394 W/m2 then compared to absorbed solar insolation of only 235 W/m2. There is no real energy balance here. They just absorbed 350 W/m2 of surface emitted IR radiation in the atmosphere and arbitrarily added only 165 W/m2 of IR-emitted energy from the atmosphere into space to the 40 W/m2 from the surface through the atmospheric window and to the 30 W/m2 from condensation of water in clouds. These numbers just appeared to be jiggered to provide apparent power flux conservation for solar insolation with the radiation of the Earth as a whole into space and to provide the right sum of power flux numbers into the atmosphere and into the surface, but without actually providing total consistency and total power balance.
It is also interesting to note that the 78 W/m2 of evaporative cooling of the surface is not matched by the heat generated in clouds when that same water condenses to produce the heat of condensation! Of course that remaining heat due to condensation could fall to the surface as warm rain, but where is that in the diagram? It turns out that they added all of that power to help generate a large back radiation component.
The discussion in my post The Greenhouse Gas Hypothesis and Thermal Radiation -- A Critical Review will make it clear that the flux of photon energy from cooler to warmer bodies does not occur as imagined in the Kiehl-Trenberth Earth Energy Budget for fundamental reasons made evident by a careful examination of cavities in radiative thermal equilibrium and the property that a thermally radiating surface in vacuum must have a photon energy density immediately outside its surface which is given by aT4, where a is Stefan's constant.
I have noted
before that a very critical aspect of our atmosphere is that the lower
troposphere part of the atmosphere disrupts the thermal radiative equilibrium between the surface and
space. It is well up into the atmosphere
at an effective altitude of about 5.1 km that radiation significantly dominates and other heat
transport mechanisms become significantly less important than radiation. Yet, the K-T diagram inverts this
relationship and claims that radiation fluxes in the lower atmosphere dominate
all other energy transport mechanisms and actually transport larger amounts of
energy back and forth by far between the lower troposphere and the surface than
they do in the upper atmosphere and back into space. This is an incredible distortion of the
reality.
Let us return to the difference in the radiative cooling due to the daily high and low temperatures. Radiative cooling was 18.5% more efficient at the daily high of about 294.25 K at mid-latitude BWI Airport than it was at the daily low average of about 282.05 K. Radiative cooling at the daily average high is about 8.8% more efficient than at the average temperature, while radiative cooling at the daily low is about 8.2 % less efficient than at the average temperature. The daily cycle radiative cooling boost for Earth based on a simple average of these high and low cooling efficiencies is only an increase in average radiative cooling efficiency of 0.3% compared to that at the daily average. For most purposes in our discussion to follow, this is a small effect and can be ignored. It is not so small when one begins to discuss the effects of increasing the concentration of CO2 in the atmosphere, however. For now we will note that 195 W/m2 of surface radiative cooling we calculated above based on the average temperature may really be more like 196 W/m2, so we will henceforth take 196 W/m2 as a more accurate daily average.
The Temperature Gradient in the Troposphere Due to Gravity and that due to Convection
Let
us also recall that there is a warming effect caused by gravity acting on the
gas molecules of the atmosphere between the altitude in the atmosphere in
radiative equilibrium with space and the Earth’s surface, which is not in
radiative equilibrium. This is because
the potential energy of a gas molecule at 5000 meters altitude added to its
kinetic energy equals the kinetic energy at sea level, assuming we set the
potential energy to zero at sea level.
Then there is a linear gradient in kinetic energy with altitude. The temperature of a perfect gas molecule is
proportional to its kinetic energy, so an increased kinetic energy at sea level
compared to its kinetic energy at 5000 meters altitude means the gas molecule
is warmer at sea level.
EK = (3/2) kT, where EK is the kinetic energy for a perfect monatomic gas molecule, where k is the Boltzmann constant. However, the lower atmosphere is made up almost entirely of diatomic molecules, with N2 and O2 more than 99% of the atmosphere. EK = (5/2) kT for a diatomic perfect or ideal gas molecule and (6/2)kT for a polyatomic molecule with more than two atoms. This is because a diatomic molecule has rotational kinetic energy around each axis perpendicular to the bond between the two atoms in the molecule. There are equal amounts of energy in each of the 5 degrees of freedom of the diatomic molecule. Molecules such as CO2 and CH4 with more than two atoms have 6 degrees of kinetic energy freedom. This allows us to tie the total kinetic energy at an altitude to the translational velocities of molecules given in the U.S. Standard Atmosphere table of 1976 for dry air. The total kinetic energy of the diatomic molecules making up more than 99% of the lower atmosphere is then 5/3 times the translational kinetic energy.
EK = (3/2) kT, where EK is the kinetic energy for a perfect monatomic gas molecule, where k is the Boltzmann constant. However, the lower atmosphere is made up almost entirely of diatomic molecules, with N2 and O2 more than 99% of the atmosphere. EK = (5/2) kT for a diatomic perfect or ideal gas molecule and (6/2)kT for a polyatomic molecule with more than two atoms. This is because a diatomic molecule has rotational kinetic energy around each axis perpendicular to the bond between the two atoms in the molecule. There are equal amounts of energy in each of the 5 degrees of freedom of the diatomic molecule. Molecules such as CO2 and CH4 with more than two atoms have 6 degrees of kinetic energy freedom. This allows us to tie the total kinetic energy at an altitude to the translational velocities of molecules given in the U.S. Standard Atmosphere table of 1976 for dry air. The total kinetic energy of the diatomic molecules making up more than 99% of the lower atmosphere is then 5/3 times the translational kinetic energy.
Conservation of energy for a diatomic gas molecule requires that:
EK0
= (5/3) (½ m v02 ) = EK5000 = (5/3)(½ m v50002
) + mgh,
Where EK0 is the energy of the gas molecule at sea level, v0 is its translational velocity there, EK5000 is the energy at 5000 meters altitude, v5000 is the translational velocity of the gas molecule at 5000 meters altitude, m is the mass of the molecule, g is the gravitational constant at 5000 meters altitude, and h is the altitude, here 5000 m. From the U.S. Standard Atmosphere table of 1976, the mean gas molecule in the atmosphere has a mass of 28.964 amu or 4.8080 x 10-26 kg, which is greater than the mass of the most common N2 molecules and lower than the mass of the second most common O2 molecules. The gravitational constant at 5000 meters altitude is slightly less than that at sea level and is found in the table to be 9.7912 m/s2. The translational velocity of the mean molecule at 5000 meters altitude from the table is 432.31 m/s. From this, we calculate that v0 is 495.62 m/s. The U.S. Standard Atmosphere sea level velocity is 458.94 m/s, implying that other effects are providing significant cooling of the atmosphere at sea level. The value of EK0 is calculated to be 9.8419 x 10-21 Joules per mean molecular weight air molecule at sea level.
We can now set the gravitational effect EK0 kinetic energy into the EK = (5/2) kT equation and calculate what T should be if there were no other cooling effects, such as the evaporation of water. Note that air convection is not a net changer of the energy here, except for the effect of volume expansion cooling as the warm air rises and the pressure drops. The temperature gradient exists in the static air, yet there is no flow of heat. We find that the surface of the Earth, at sea level, should have a temperature of 285.07K, or 11.92ºC, or 53.46ºF, which is 30.1K warmer than the 255K it would have if the surface itself were in direct radiative equilibrium with space as a black body, assuming a nearly constant temperature throughout a day. Of course the Earth is not a black body as we discovered and with an emissivity of 0.5 and an absorbed solar insolation of 186 W/m2, the expected surface temperature is 284.61K, or about the same temperature as is expected given its thermal equilibrium with the bottom of the atmosphere at 285.07K. Thus the bottom of the atmosphere expected temperature due to the static equilibrium gravitational field effect is only 2.58K less than the commonly quoted average surface temperature of the Earth and the Earth’s surface itself is only 3.04K less than the average surface temperature.
From the U.S. Standard Atmosphere table of 1976 for dry air, the temperature at 5 km altitude is 255.68K. If the surface temperature were 285.07K, the effective lapse rate per 1 km elevation between 5 km and sea level would be 5.88K/km. Weighting monatomic, diatomic, and polyatomic molecules for the relationship of their total kinetic energy to their translational kinetic energy and weighting the total kinetic energy relation to the temperature, the calculated static gravitational gradient increases slightly to 5.93K/km. Using this gradient, the surface temperature would be 285.33K. This still has errors due to treating each molecule as having the mean weight and mean velocity. Of course the surface temperature is slightly higher at 288.15K, so the static equilibrium gravitational gradient is really 6.49K/km. This difference between 5.93K/km and 6.49K/km is not due to water vapor in static air. Water vapor has a large effect upon the dynamic adiabatic lapse rate, but a small effect upon this static equilibrium temperature gradient due to gravity alone. Adding water decreases the mean molecular weight and increases the fraction of molecules with 6 degrees of freedom, but there is so little water usually that the effect on this temperature gradient is still small.
At this point, one might ask if the U.S. Standard Atmosphere table of 1976 is consistent with the ideal gas law of PV = nRT? It is. If we examine the case for 1 m3 of air at sea level and for the same volume at 5000 m altitude, we have
T5000 / T0 = (n0P5000)
/ (n5000P0) = (δ0P5000) /
(δ5000P0),
where δ is the density of the atmosphere at the given altitude. The table provides δ0 = 1.2250 kg/m3, δ5000 = 0.73643 kg/m3, P0 = 1013.25 mb, and P5000 = 540.48 mb, with mb being millibars. The table provides the surface temperature at sea level as 288.15K, and the ratio formula above then says the temperature T5000 = 255.674, in agreement with the table value given as 255.676K. The fact that the molecule energy conservation formula used above that yielded a surface temperature of 285.07K was slightly different than 288.15K is the measure to which the air does not represent quite a perfect and ideal gas primarily, but secondarily to the neglect of the slightly less than 1% of gases which are almost entirely monatomic molecules and have only translational kinetic energy. The neglect of the monatomic gases would have dropped the surface temperature slightly, though most of this difference is due to a small deviation of air from being a perfect gas.
The theoretical thermodynamic derivation of the gravitational temperature gradient along an adiabatic pathway is commonly given to be g/Cp after a correction to a derivation by Loschmidt in the 19th century, where g is the gravitational “constant”, varying from 9.8066 to 9.7912 m/s2 between sea level and 5 km altitude. Cp is the heat capacity at constant pressure of dry air, which between 250K and 300K increases from 1.003 to 1.005 KJ/kgK. Consequently, the lapse rate calculated from the g/Cp formula is 9.76K/Km. If we applied that lapse rate to calculate the Earth’s surface temperature with respect to the approximately radiative equilibrium temperature at 5 km of 255.68K, we would have a higher average surface temperature of 304.7K, which is 16.5K warmer than the actual surface temperature.
Consequently, we can conclude that the prediction of a lapse rate of g/Cp is not applicable to the atmosphere for its equilibrium condition as static atmosphere. Indeed, Loschmidt made his calculation on the basis that gravitational heating would cause warm air at lower altitudes to rise and that in doing so he should follow a given number of moles of gas as it rose. As a consequence, the volume expansion of the gas as it rises causes it to cool on top of the static gravitational temperature gradient, so his prediction of the equilibrium temperature gradient is substantially too large for the static air condition. Indeed, the adiabatic pathway in a Carnot cycle for a perfect gas implies both a change of pressure and of volume for the gas. The temperature gradient calculated on the basis of energy conservation exists with still air and will be modified by dynamic conditions such as convection and wind due to energy gradients. The dynamic condition envisioned by Loschmidt occurs because of an energy gradient. The static air equilibrium temperature gradient occurs within an equal energy column of air. To calculate the static temperature gradient due to gravity, we must remember that temperature is an intensive, not an extensive parameter. Temperature is due to the energy of a molecule of gas, at least if it is a perfect and ideal gas as air nearly is. We are of course talking about a mean molecular energy in a given volume of air.
Of course in the real world, the static air equilibrium temperature gradient is a baseline and as we know air does rise by convection in variable amounts through a day. To the extent that air in our observed column has large amounts of air from the bottom rising and then expanding as it will often do under normal unstable conditions, an additional rate of cooling will occur. When all the air in the column is moving adiabatically, then the Loschmidt temperature gradient of about 9.78K/km will apply. For intermediate levels of air convection, the temperature gradient will vary from 6.49K/km to 9.78K/km. We also know that when the moisture content of air is high, it is lighter and upward convection tends to increase due to even less perturbation. The convection of moist air will affect the temperature gradient.
Heat Transport Mechanisms in the Lower Troposphere
Note that
this large surface warming by the action of the gravitational field depends
upon the surface not being in radiative equilibrium with the upper
atmosphere. It is the high density of
our atmosphere that produces this condition, in conjunction with the fact that
the mean free path for infrared absorption at the wavelengths that water vapor
and carbon dioxide absorb is short compared to the thickness of the atmosphere due to the already substantial
concentrations of water vapor and carbon dioxide. The absorption mean free
path for carbon dioxide is variously reported as 25, 33, and 47 m. That for water vapor is more variable, but on
average it is said to be much shorter with an average value near 8 m. These really short values of the mean free path appear to be based on measurements which cannot be transferred to the case of the atmosphere. Measurements made with infra-red sources at much higher temperatures than the absorbing molecules provide a well-defined mean free path which is not applicable to the continuous and slight temperature gradient found in our atmosphere. Nonetheless, the variable mean free path dependent upon both temperature and number density of the emitting and absorbing molecules is short enough that the IR surface emission energy at wavelengths water vapor and
carbon dioxide can absorb is subject to dissipation amongst the more common
nitrogen and oxygen molecules where the collision frequency is high enough that
re-emission as IR radiation takes many times longer than the mean time between gas
molecule collisions. This rapidly brings
the so-called greenhouse gases into thermal equilibrium with the local air temperature, which
falls with altitude.
The fact that water evaporation and transport and air conduction, convection, and wind keep the surface from being in radiative equilibrium with the upper atmosphere is essential. Yet, there must also be infrared-emitting molecules in the upper atmosphere in sufficient quantity to establish a radiative equilibrium with space equalling our primary heating source, the Sun, above a lower atmosphere in which slower heat transfer mechanisms dominate. On Earth, this condition is established by our plentiful nitrogen, oxygen, and argon filled atmosphere and the presence of the dominant water vapor infrared emitter. The altitude in radiative equilibrium with space is primarily dependent upon the density of the lower atmosphere non-radiating gases and the rate of density change with altitude and the upper range of the dominant IR-active gas, water vapor. The doubling of a minor IR-absorbing and emitting gas such as carbon dioxide has little effect upon the altitude of the sphere in effective radiative equilibrium with space, especially when it emits from much higher altitudes and on the border with the tropopause.
The fact that water evaporation and transport and air conduction, convection, and wind keep the surface from being in radiative equilibrium with the upper atmosphere is essential. Yet, there must also be infrared-emitting molecules in the upper atmosphere in sufficient quantity to establish a radiative equilibrium with space equalling our primary heating source, the Sun, above a lower atmosphere in which slower heat transfer mechanisms dominate. On Earth, this condition is established by our plentiful nitrogen, oxygen, and argon filled atmosphere and the presence of the dominant water vapor infrared emitter. The altitude in radiative equilibrium with space is primarily dependent upon the density of the lower atmosphere non-radiating gases and the rate of density change with altitude and the upper range of the dominant IR-active gas, water vapor. The doubling of a minor IR-absorbing and emitting gas such as carbon dioxide has little effect upon the altitude of the sphere in effective radiative equilibrium with space, especially when it emits from much higher altitudes and on the border with the tropopause.
Of course there is no sharp shell at 5100 m which absorbs all solar insolation and emits all the outgoing infrared radiation as from a simple black body radiator shell. But, in trying to cut through the many complexities of the Earth’s temperature balance, such a picture makes very good sense for the purpose of understanding and estimating the first-order effects on the Earth’s surface temperature. It offers a simple model which allows the primary means of transferring energy by water evaporation, gas molecule collisions, and other non-radiative effects to operate where they are the major factors. IR radiation becomes a primary factor only above about 4000 meters altitude. Of course, there are frequency windows in which most of the IR radiation emitted at the Earth’s surface can escape straight into space.
IR radiative cooling of the Earth by so-called greenhouse gases is strongest from about 4000 to about 11000 meters altitude and with the temperature dropping throughout the troposphere with increasing altitude, radiative cooling becomes less and less efficient. But it is rapid compared to the cooling effects of the lower troposphere. Data from the NIMBUS satellites of the Earth’s emission spectrum into space show that the dominant water vapor emission is mostly from altitudes from 2.5 km to 6 km, CO2 emission is from 3.5 km to 20 or more km with most of it in the beyond 10 km altitude, and methane and nitrous oxide radiate mostly from 2 to 4.5 km altitude. The methane and nitrous oxide tend not to build up, since they are quickly broken down by UV radiation. Note that because CO2 reabsorbs its emissions at lower altitudes or often has those emissions reabsorbed by water vapor, it is only from the upper edge of the troposphere that CO2 emissions manage to reach space. The temperature at the top of the troposphere has fallen to a frigid 217K. As a result, the altitude with the temperature matching the thermal equilibrium seen from space of 255 K is found at the top of the water emission zone at about 5100 m.
Having taken into account the fact that the surface emissivity is close to 0.5, rather than the black body value of 1.0, the temperature gradient in the troposphere due to gravity, and understanding that radiative cooling of the Earth as a whole occurs mostly from the top of the high concentration water vapor portion of the atmosphere, we need to examine more issues relating to adding more of an IR-active gas to the atmosphere and to more issues relating to backscatter radiation warming of the surface. We also need to appreciate the ability of non-radiative cooling mechanisms to keep mid-day temperatures at the surface from soaring. It is clear that the major actors in explaining this mid-day cooling are the evaporation of water at the surface, conduction of heat across a thin layer of air very near the surface, and air convection and winds toward the cooler polar regions. As noted, there is infrared surface emission cooling also.
The Absorption of Solar Insolation in the Atmosphere
We need to discuss the effects of the atmosphere upon incoming solar radiation. Rayleigh scattering by the atmosphere shields the surface of a substantial portion of the UV and short wavelength visible portion of solar radiation. Ozone shields the surface from further UV radiation. Water vapor and oxygen have absorption bands in the long wavelength visible portion of the solar spectrum.
When discussing any effects of IR-absorbing gases, one needs to take into account the absorption of IR radiation incident on the Earth's atmosphere from the sun, which is commonly very cavalierly not considered in comparison to the back-reflection argument by strong greenhouse gas effect advocates. This is important, since much of the sun's IR radiation does reach the Earth's surface and does warm it directly, though some is also absorbed in the atmosphere before reaching the surface. In addition, some of the sun's IR radiation is reflected by the surface, instead of being absorbed, so it does not directly warm the surface. So, the question arises: Do these IR-absorbing gases in the atmosphere result in a net warming or cooling of the Earth's surface? If the absorption of solar insolation is minimal and the back-radiation is as large as the man-made global warming advocates have often claimed it to be, it might have a warming effect. Of course we now know that if it has a warming effect, then there must be more cooling by air conduction and convection and by water evaporation than they claim there is, since we now know that direct solar insolation absorbed and the equilibrium temperature gradient due to gravity is sufficient to explain why the surface temperature is about 15ºC.
First of all, let us enlarge the context of the discussion. The primary source of heat for the surface of the Earth is the radiant energy of the sun. The solar wind of the sun, materials dumped into the atmosphere from space, heat from the deep interior of the earth, the interplay of changes in the Earth's magnetic field and the sun's magnetic field, frictional warming due to winds across the surface, the energy from the tidal effects of the gravitational interaction with the moon and the sun are also contributors of energy or heat, though the sum of these is very small compared to the sun's radiant energy spectrum of ultraviolet (UV), visible, and infrared (IR) light. Nonetheless, in conjunction with the very important variations in cloud cover and the less important effects of blown dust and volcanic emissions these natural effects cause some of the variability in the energy supply that affects the Earth’s surface temperatures.
The common explanations for a catastrophic greenhouse gas hypothesis claim the effects of the greenhouse gases upon the much more energetic incident UV, visible, and IR portions of this spectrum of radiation from the sun are negligible. It is hard to comprehend how this critical effect is given little attention and is so underestimated. A contributing reason is probably the fact that a small percentage absorption from the solar insolation spectrum is likely to occur in a much higher energy portion of the radiative spectrum compared to the Earth’s surface emission spectrum. Therefore the equivalent power percentage of the much lower power spectrum of the Earth’s emissions would be large.
UV light is 11% of the radiant energy from the sun, if the UV range is that below 400 nm. The UV light variance of 0.5 to 0.8% with the solar cycle is much larger than is the visible light variance of 0.22%. UV light is absorbed throughout the atmosphere, but much still reaches the ground and is absorbed there. The amount of UV radiation absorbed in the upper atmosphere is dependent upon the amount of ozone there. The amount of ozone is said variously to be dependent upon the solar wind, CFCs, water vapor, and volcanic activity. When UV light is more absorbed in the stratosphere than the ground, its surface warming effect is greatly diminished. Much of the absorbed energy is re-emitted as UV radiation and half of that energy is quickly lost to space. Nonetheless, much of the UV light energy is absorbed by the ground. In addition to the absorption of UV by ozone, it is also absorbed and re-emitted by electronic transitions by nitrogen, oxygen, argon, and carbon atoms.
It is often incorrectly said that the entire atmosphere is transparent to visible light which is the form of 40% of the radiant energy from the sun, taking visible light from 400 to 750 nm. Most people can actually see visible light from 370 to 770 nm and I can see it from at least 354 to 794 nm. Because of this, the visible light range is taken differently in different accounts.
Visible light is reflected from clouds and aerosol particles, but as we will see below, a considerable fraction of the visible light does not reach the ground or oceans to warm their surfaces even when the sky is clear. O2, atomic oxygen, and O3 absorb solar UV light. O3, O2, and H2O absorb some visible light from the solar insolation. The main O2 absorption is just about at the boundary between visible and infrared radiation, though I can personally see that wavelength. Water vapor and carbon dioxide are the main absorbers of solar insolation in the near (shortwave) infrared solar spectrum. The UV radiation is of higher energy than the visible light and the visible light is of higher energy than the near infrared radiation. The excitation of electronic transitions occurs in argon, carbon, oxygen, nitrogen atoms in the visible light range, so one has to consider these absorptions in addition to the vibrational molecular absorptions considered for water vapor.
We can see the absorption effects of the main atmospheric gases below, where shorter wavelength is higher energy. The UV portion of the spectrum is from 0.1 to 0.4 µm wavelength, the visible portion is from 0.4 to 0.75 µm wavelength, and the near infrared portion of the spectrum is from 0.75 to 3 µm wavelength. This covers the portion of the energy spectrum in which the solar insolation energies are important. Radiation from the Earth’s surface due to its temperature has a spectrum that peaks in the mid-infrared spectrum and has a significant tail into the far-infrared (longwave) spectrum. This emission spectrum is in a much lower energy range than is the solar insolation spectrum.
Finally, mid-IR radiation (3,000 to 30,000 nm) is not absorbed by nitrogen, oxygen, and argon gases which make up 99% of the atmosphere. A large fraction of the solar IR directly warms the Earth's surface. Substantial amounts are absorbed by the dominant IR-absorbing gas, water vapor, and small amounts are absorbed by the very low concentration gas carbon dioxide. Methane and nitrous oxide mostly absorb the lower energy, longer wavelength infrared emissions from the Earth’s surface.
The incoming IR radiation absorbed in the atmosphere is much less effective in warming the Earth's surface than is that which is absorbed by the Earth's surface directly. This is because much of the absorbed energy locally warms a mass of air and it then rises as it expands and becomes more buoyant. Some of this energy absorbed in the atmosphere then is radiated again as IR radiation directed upward only to be quickly absorbed by the dense atmosphere and again converted into rising convection. In other words, more water vapor and CO2 in the atmosphere results in a less effective warming of the surface because incoming solar energy is kept far from the surface. The principal IR-absorbing gases of water vapor and carbon dioxide have a cooling effect on the ground on the original solar radiance spectrum for portions of the 49% of the solar energy in the IR frequency range. This energy is still being deposited in the Earth's atmosphere, but has a much reduced effect in warming the Earth's surface.
A mid-day solar light spectrum outside the atmosphere and the solar radiance spectrum transmitted through the atmosphere to sea level in the South Pacific are shown in Fig. 4. The outside the atmosphere solar spectrum is not quite that of a black body at the near surface temperature of the sun, because some absorption in radiation from the sun occurs in its cooler surface plumes, the solar wind, and by the extremely low concentration gases of the solar system due to the large distance from the sun to the Earth.
The measurement of the transmitted energy from space to the Earth’s surface and its distribution with wavelength is highly dependent upon the amount of water vapor in the atmosphere, so the transmitted spectrum may vary considerably, but the spectrum shown is fairly typical. But, for the purposes of this discussion, let us use the overall transmittance values to the Earth's surface from this graph of an actual particular measurement. This is not an average, but it makes the point that such real effects must be accounted for and have a major impact on the argument of whether IR-absorbing gases heat or cool the surface of the Earth. The overall energy transmittance is about 0.65, which is in good agreement with the accepted average. The transmittance of UV and Visible radiation combined is about 0.59, while that for IR radiation is about 0.69 according to the limited range of the graph in Fig. 4. The total fraction of the solar insolation incident at the top of the Earth’s atmosphere and transmitted by the atmosphere and incident upon the surface here is then (0.59)(0.51) + (0.69)(0.49) = 0.64, which shows the breakdown by portions of the spectrum to be within round-off error of the overall transmittance. This is slightly higher than the 0.58 fraction of the Kiehl-Trenberth diagram in Fig. 2, but in good agreement with many other sources.
The 31% loss of solar insolation IR radiation in the atmosphere measurable from Fig. 4 is due to water vapor and CO2. However, absorption in the long IR tail beyond the 2700 nm cut-off on Fig. 4, shows much higher IR absorption in that tail. These IR-absorbing gases are keeping at least 31% of the 49% of the solar radiation due to IR from reaching the Earth’s surface. Thus, at least (0.31)(0.49) = 0.152 of the total solar IR radiation incident upon the top of the atmosphere does not reach the ground because of IR absorption. But due to the neglect of the long IR tail with its higher level of absorption due to water vapor and CO2, a better value for the fraction of the solar insolation IR absorbed by the atmosphere is 19%, which is pointed out in the very useful paper by Klaus Ermecke entitled Rescue from the Climate Saviors, published in June 2010 by KE Research.
This provides a sizeable cooling effect upon surface temperatures attributable to the so-called greenhouse gases of water vapor and carbon dioxide. If they did not absorb this solar insolation, the additional power incident upon the surface would be (0.19)(342 W/m2) = 65.0 W/m2. Add this to the 219 W/m2 (64% of 342 W/m2) actually incident upon the surface and assume that the surface reflectivity is still 15.2% as used by K-T in Fig. 2., then the total power absorbed by the surface would be (1 - 0.152) (219 + 65) W/m2 = 241 W/m2. With a surface emissivity of 0.5, this would make the surface temperature 303.6K. This means that the absorption of incoming solar radiation by water vapor and carbon dioxide is a 16.0K cooling of the surface. This is substantially more than the IPCC claim for the temperature rise due to doubling the CO2 concentration in the atmosphere of 5.4K with strong positive water vapor reinforcement. This brings home the critical need to account for additional cooling absorption of the IR portion of solar insolation due to changes in the water vapor and carbon dioxide concentrations in the atmosphere.
Further increases in the CO2 concentration will add to this cooling effect by preventing still more solar insolation in the IR range from reaching the surface. What is more, the claimed 5.4K temperature increase due to doubling the CO2 concentration depends upon the correctness of the IPCC claim that there is a strong positive feedback causing water vapor increases. Water vapor increases are said to cause all but 1.2K of that 5.4K temperature increase.
If it were true that water vapor did increase due to increased CO2, then water vapor would definitely block more surface absorption of solar insolation as an IR-absorber and it would generate more cloud cover, which would reflect more solar insolation from well up in the atmosphere off into space. Cloud cover is a powerful coolant for the surface temperatures. These effects of added water vapor make it most unlikely that water vapor has a strong positive feedback effect upon increased carbon dioxide supposed warming. That additional water vapor is a powerful coolant in the lower atmosphere is also well known from the fact that the humid air lapse rate, the measured temperature gradient with altitude, is lower than the dry air lapse rate. Indeed, the added IR absorption of solar insolation caused by CO2 itself would reduce the amount of warming CO2 might produce by some other mechanism.
Fig. 5. The percentage of blue sky observed by
satellite between 1983 and 2009 from the paper by Klaus Ermecke, Rescue from
the Climate Saviors, June 2010, KE Research.
Note that the blue sky percentage was low in the cooler 1980s, was high
in the warming period after 1996, but has been falling slightly since about
2002 as the warming has paused. The
range of variation is from about 30.5% to 36%, with the high about 18% greater
than the low. Bigger variations have
likely occurred in the past. At least in
this time frame, increased cloud cover correlates with cooler surface
temperatures, which is hardly surprising.
Increased water vapor in the atmosphere will generally form more
clouds
as rising warm air cools and the water vapor condenses.Thus, increased
water vapor owing to warming effects already underway produces more
cloud cover, which cools the Earth's surface. The general effect of
increased water vapor is both to absorb and to reflect more of the solar
insolation before it reaches the surface. This cools the surface and
demonstrates the usual negative feedback of water vapor to warming
caused by other factors such as increased solar insolation at the top of
the atmosphere or any possible increase due to increased carbon
dioxide.
In each case, whether UV, visible light, or IR, not all of the radiation of that form striking the Earth's surface is absorbed. Some fraction is reflected and the fraction is very dependent on whether the ground is covered with snow, plowed earth, grasses, forests, crops, black top, or water. There are real ways that man does have some effect on the Earth's temperature. He changes the surface of the earth over a fraction of the 30% of its surface which is land, affecting its reflectivity, its contributions to evaporative cooling, thermal convection, and its local emissivity. He also converts fossil and biomass fuels into heat. The carbon black and other small particles he releases into the atmosphere and some aerosols man generates, also have some impact on the temperature at the Earth's surface. His use of the land may affect the amount of dust which is blown, sometimes for long distances. Compared to the overall natural effects, these man-made effects are small, yet they may be larger than the effect of man adding CO2 and methane to the atmosphere for reasons we have and are about to further develop.
In the outer, low density atmosphere, the primary means of heat transfer is radiant transfer by IR emission from an energetic molecule or atom, since collisions of molecules and atoms for direct energy transfer have mean times between events greater than the time between an IR-absorbing gas absorbing and then re-emitting IR radiation. In the denser, lower altitude atmosphere, most energy transfer is due to gas molecule collisions and the convective flow of masses of warmed air. Near the Earth's surface, much of the energy lost by the warmed surface is due to gas molecules striking the surface and picking up heat and then colliding with other molecules to transfer heat from one to another or due to the evaporation of water. Radiative cooling of the surface is important, but due to IR-absorbing gas molecules such as water vapor and carbon dioxide, most of that energy is reabsorbed by the atmosphere only a few tens of meters from the surface. This means there is a bit of a speed up in the removal of heat in that IR over those few tens of meters travels at the speed of light, not at the speed of air convection currents or wind. That portion of the surface emission spectrum not absorbed by IR-absorbing gases is simply emitted off into space at the speed of light. Thus, radiative cooling is extremely efficient without greenhouse gases, but still efficient with them when compared to air convection. This radiative efficiency in cooling is very apparent in dry deserts and at high elevations on a mountain in the night and is easily experienced.
Once a body of air near the surface is heated, then masses of warmed air molecules are transported upward into the cooler atmosphere at higher altitudes or laterally toward cooler surface areas by convection or wind. Warmed molecules, most of which are nitrogen, oxygen, and argon, will act to keep the rarer water vapor and carbon dioxide molecules at the same temperature they are at for a particular altitude. These water vapor and other IR-absorbing molecules will emit IR radiation in the mid and far infrared ranges. However, no molecule or atom at a low temperature such as that near the Earth's surface is a very effective energy radiator, since the Stephan-Boltzmann equation depends upon the fourth power of the absolute temperature, which commonly near the Earth's surface is about 288K. As molecules rise in altitude, their temperature falls and they become still less efficient IR emitters. The number of such emitters falls as the atmospheric density falls, but the mean free path before re-absorption of an emitted photon occurs becomes longer. Thus, gas molecule collisions and convection and the evaporation of water and its transport are the dominant means of heat transfer in the dense atmosphere near the surface. These processes on balance cool the surface of the Earth and redistribute some of the heat back into the upper troposphere and cooler places such as those shaded from the sun or in arctic regions.
Substantial Surface Radiation Power Conversion to Other Cooling Mechanisms
You might be thinking there is a contradiction in the above paragraph in which I say that water evaporation and air convection are the primary means of energy transport, but earlier I said that the radiation from the surface was as great as 196 W/m2. First of all, because this is not surface emission into a vacuum, the radiation potential given by the Stefan-Boltzmann equation is not realized. Other cooling mechanisms remove much of the energy that would otherwise be radiated into a vacuum. Even that portion which is radiated as IR is soon converted into energy transport by convection. This is because the absorption length for that part of the emitted surface radiation which can be absorbed by so-called greenhouse gases in the lower atmosphere is short. Absorbed energy is soon spread to the far more plentiful non-IR-absorbing gases due to the very high collision rates in the troposphere..
The partitioning of the energy between radiation and both conduction and convection changes rapidly even in the first few hundred meters above the surface. It has been reported that the mean free path for IR radiation absorbed by water vapor at sea level is only 8 m and that for carbon dioxide is 47 m according to the calculations of Nasif Nahle in his July 2010 paper entitled Mean Free Path of Photons through the Troposphere and Time of Crossing Path of Photons Leaving the Troposphere Without Colliding with a Molecule of Carbon Dioxide and/or a Molecule of Water Vapor. As I noted above, these very small values for the mean free path may only be appropriate for cases with a much greater temperature differential between the emitter and the absorber molecules. Nonetheless, even a mean free path length of 2000 meters for water vapor would still keep the surface from being in radiative equilibrium with the upper altitudes of the troposphere which can be in radiative equilibrium with space. This is all that is needed to allow the temperature gradient due to the atmospheric lapse rate to shift surface temperatures to levels well above the equilibrium temperature of 255K with space.
When coupled with a high molecular collision rate of 6.92 billion collisions a second at sea level, surface radiative energy is rapidly converted into much slower moving energy transport by air conduction and convection. Consequently, the height above the surface at which the measurements of surface radiation versus air conduction and air convection are made will result in large variations in the partition of energy transport between these mechanisms. A measurement made 1 meter above the surface will differ greatly from one made 500 meters or 2000 meters above the surface in the ratio of surface radiation to air conduction and convection. It will also depend strongly upon the humidity of the air.
The solar irradiance has a power density just outside the atmosphere of the Earth of about 1367 W/m2. We saw from the discussion of the transmittance spectrum of the sun's radiation that the overall energy reaching the surface is about 0.65 times the total energy outside the outer atmosphere. So 0.65 times 1367 W/m2 is 888.6 W/m2, which reaches the Earth's surface. Of this energy, about 15.2 % is reflected from the Earth's surface without being absorbed according to the Kiehl-Trenberth energy balance diagram above.
Thus, the energy warming the surface is the absorbed power density of about 753.5 W/m2 at the time of maximal solar insolation during an average day. With a surface emissivity of the Earth of 0.5, the temperature of the surface would be 404K or 131ºC, were it not for conduction of heat into the subsurface, evaporation of water, and air conduction and convection cooling of the surface! Such a temperature would be fatal for humans and most of the Earth’s surface life-forms. Humans would be boiled to death. This tells us how critically important it is that these surface cooling mechanisms are very powerful when they need be. Since the daily high is rarely higher than about 106ºF or 314 K, except in some very dry areas, these cooling mechanisms can generally lower the surface temperature by more than 90K.
If the surface radiation were the strong surface cooling effect shown in the Kiehl-Trenberth Energy Budget to altitudes of thousands of meters and back radiation from the atmosphere existed at the hugely exaggerated power densities shown in that diagram, some very interesting and terrible things would happen at mid-day. Just taking the absorbed power ratio to the surface emitted power ratios would give (753.5 W/m2) / (168 W/m2) = P / (390 W/m2), so P = 1749 W/m2 would be the heat radiated by the surface at mid-day if the Kiehl-Trenberth Energy Budget were right.
Assuming human skin absorbs all such IR radiation as the K-T model claims the Earth's surface does, then such mid-day surface radiation would surely cook our goose! Since we are largely water-based organisms, as are plants covering most of the land surface, we ought to have similar absorption properties to those they claim the land portions of the Earth have. Standing in bright mid-day sun we have all felt the substantial warming of the 753.5 W/m2 from the direct line with the sun, but we do not feel the even greater 1749 W/m2 coming up from the ground we should expect under the K-T physics.
Dissipation of Surface IR Emission Heat by IR-Active Gases and Collisions
Let us next examine the portions of the Earth’s radiation spectrum which are absorbed and re-emitted by IR-active gases so we can better assess claims of a large back-radiation effect, despite the fact that such an effect would force us to posit compensating non-radiative cooling effects. See Fig. 6. below.
Fig. 6. The red spectrum of UV, visible light, and near infrared radiation is that from the sun and incident upon the Earth, while the blue spectrum at the top of the diagram is the mid and far infrared radiative spectrum of the Earth. The outer curves are those of black body radiators at the stated temperature, while the interior solid red spectrum is the radiation incident upon the Earth’s surface and the solid blue spectrum is the radiation from the surface which is not absorbed by the atmosphere. It is critical to note that there are two deceptions in this figure. One is that the area under the solar energy spectrum incident upon the surface is about four times greater than the area under the Earth surface emission spectrum. The other deception to the eye is the fact that the wavelength is given on a logarithm scale. This compresses the wavelength on the right side of the scale. Because the energy of a photon is proportional to the inverse of the wavelength, this means the energy scale is stretched out on the right side. This makes it appear that IR-active gas absorption is much more important an effect on the emission side than on the solar insolation side. The figure clearly shows that the Earth’s surface is not in radiative equilibrium with space due primarily to absorption by water vapor and very secondarily due to absorption by carbon dioxide. Note that the solid blue radiation spectrum is not all the energy which is emitted into space, but only the part that was emitted from the surface into the atmospheric window. The radiation absorption spectra due to various absorption mechanisms are shown in the lower portion of the diagram, with their absorption sum shown above. The absorption effects of water vapor and carbon dioxide are both fully saturated over the majority of the Earth’s emission spectrum.
Note that the solar radiation absorption spectrum at the top left shows somewhat less absorption than the actual measurement in Fig. 4. This probably reveals that there is some shortcoming in the approach of trying to reconstruct that absorption from the separate absorption spectra of the gases considered here. Nitrogen gas, which is 78.084% of the atmosphere, is entirely left out, because it is not an infrared absorber. Perhaps it has ionization products and dimer or trimer products with water that do absorb, however. There is reason to believe that CO2 and water vapor have such products. These and other similar products of other gases may account for the additional absorption that occurs in the measured solar radiance compared to the composed one of the figure immediately above. But since this data is well-respected in catastrophic greenhouse gas circles, it is fair to use it to at least show some of the limitations of the usual explanations of the catastrophic greenhouse gas hypothesis. The fraction of the long wavelength IR emitted from the ground at about 290K which is absorbed as actually shown in this graph is 0.65, though the labeling says it is from 0.70 to 0.75. We will take this fraction to be the graphed 0.65, consistent with the practice of many others.
A fraction of the gas molecules which have absorbed long wavelength IR radiation emitted from the ground will cool by emitting IR radiation in turn or by collisions with other molecules. Water vapor is the best long wavelength IR absorber and it is the best emitter of IR energy, but before it can commonly emit the energy as radiation that it has absorbed from IR radiation, even it will likely suffer numerous gas collisions with much of its excess molecular energy being transferred in those collisions to the molecules which collide with the water molecule. Nitrogen molecules are the most likely molecules to take up much of the energy from the water molecule, since nitrogen is 78.08% of the atmosphere. Oxygen molecules are the next most likely colliders at 20.95% and then argon atoms at 0.93%. Together, these three gases account for 99.97% of the U.S. Standard Atmosphere. None of these gas molecules are IR absorbers in the long wavelength, or mid and far infrared, spectrum.
At sea level, the mean gas velocity is 459 m/s, the mean free path or distance between collisions is only 6.6 x 10-8 m or 66 nm, and the collision frequency is 6.9 billion/s. The time between collisions is then about 1.45 x 10-10 s. The radiative lifetime of the 15 micrometer CO2 absorbing band is about 0.8 s. The radiative lifetime of the water vapor absorption band at 6.3 micrometers is about 0.05 s and that for ozone at 9.6 micrometers is about 0.08 s. These are times more than 100 million times the time between collisions! Consequently, essentially every absorbing molecule gives up any energy absorbed from infra-red radiation to the surrounding air molecules in its immediate vicinity before it can re-emit that energy. In the equilibrium condition, a higher altitude infra-red active molecule is always cooler then compared to the surface or lower altitude molecules. It cannot radiate photons to those warmer molecules below it. To be sure, this simple model does not take into account the molecule in the shade at a lower altitude being at a lower temperature than a molecule in direct sunlight, but above it in altitude. Neither does it account for the occasional temperature inversion in the air.
Aside from the caveats just mentioned, there is no back-radiation from the atmosphere. Then if one uses the numbers from the K-T energy budget of Fig. 2, of the 168 W/m2 absorbed, if 78 W/m2 is given up in evaporation and 24 W/m2 is lost as convection currents, the remainder to lost as infra-red radiation is only 66 W/m2. Note that this estimated contribution of sea level surface energy loss by radiation is much lower than the huge radiative losses in the K-T energy budget of Fig. 2 of 390 W/m2, of which 350 W/m2 is absorbed by the atmosphere. They believe that the total power absorbed by the atmosphere is (350 + 78 + 24) W/m2 = 452 W/m2. In reality the total absorbed by the atmosphere is only (66 - 40 + 78 +24) W/m2 = 118 W/m2, where 40 W/m2 is lost directly to space through the atmospheric window. The K-T fraction of the energy loss of the surface into the troposphere by radiation was 350/450 = 0.78. In reality, it is only 16/118 = 0.14 so the roles of water evaporation and convection in cooling the surface are hugely underestimated by K-T. The radiative transport of energy, as discussed above, actually falls off to a lower fraction of the energy transported as one moves away from the immediate surface as the 16 W/m2 is absorbed with increasing altitude.
Let me emphasize that the radiation transport is from emitters which
are essentially in thermal equilibrium with the gas molecules at its altitude
and therefore on a cooling gradient with increasing altitude. What is more, the radiation emitted is
absorbed by further molecules above which are only very slightly cooler because
they are not far above. When that
radiation is downward, the potential absorbers are usually warmer. When they are cooler, as
might be the case if that pocket of air is in the shade of a tree or
building, they may be warmed. Another case of downward
warming may be in the thin layer of air over a water surface that cooled during
the night and because of the high heat capacity of water, the air a few feet
over the water surface is warmed in the morning sun faster than is the surface of
the water or a thin layer of air immediately above the water surface.
To sum up the
situation of the power flux cooling the surface:
66 W/m2 (39% of surface cooling) leaves the surface as IR, of which 40 W/m2 is immediately lost to space.
78 W/m2 (46% of surface cooling) leaves the surface as evaporative cooling according to K-T
24 W/m2 (14% of surface cooling) leaves the surface as convection (and conduction) according to K-T
I was concerned that the 24 W/m2 of thermals at the surface according to Kiehl and Trenberth made soaring hawks, eagles, and other birds absolutely supernatural in their soaring ability, but it is clear that thermals increase with altitude within a few tens of meters over the surface and soon become substantially greater than the 24 W/m2 estimate by Kiehl and Trenberth. Unmanned gliders have been developed that use a propeller to get off the ground and to get a couple of tens of meters in altitude. Once there, they can glide all day. The air is relatively still over the featureless ocean close to its surface, but an albatross can fly thousands of kilometers without flapping its wings because the layer of air just a bit higher is moving quite nicely. The albatross can swoop and climb all day using the wind shear between the surface layer of air and the air just above it. We humans are generally not aware of these effects and are prone to underestimating them.
Now some will be reluctant to believe that the fraction of radiative cooling of the surface immediately at the interface with the atmosphere is only about 39% of the total cooling, assuming that back-radiation does no heating of the surface. Yet, Physics Prof. Robert Williams Wood of Johns Hopkins University in his classic greenhouse experiments concluded that IR radiation from solar warmed surfaces was only about 4%. Chilingar, Khilyuk, and Sorohtin concluded in 2008 that surface radiation was only about 8% of the surface cooling. The value I have given here of 39% is an upper limit since much of the radiation is soon converted into added convection.
There is no
problem with the alternative cooling mechanisms being much larger than the low values given above. We
can get some insight on that by returning to the issue of the mid-day cooling
when as much as 753.5 W/m2 is being absorbed in the surface. On a hot day, the temperature at a
mid-latitude might be 106ºF or 41ºC or 314K.
The radiative cooling upper limit is then 275.6 W/m2 with an emissivity of 0.5 and is
likely only half of that at most, given that evaporation and convection usually account for a majority of the energy loss of the surface. This
means that other cooling mechanisms, including the flow of heat into the ground
or underlying water, cool the surface with a power of about (753.5 – 0.5
(275.6)) W/m2 = 615.7 W/m2 at mid-day. At that time, the radiative cooling is not
more than 137.8 / 615.7 = 0.224 or about 22% of all the other cooling mechanisms.
Once again, this fraction of the radiative cooling may still be
influenced by a low average set of values for evaporative and convective cooling
by K-T. Consequently, it is easy to
believe that surface radiative cooling is less than 22% of surface cooling.
Let us examine Figure 6 to determine what the relative effects of CO2 absorption are on the solar insolation spectrum and on the Earth radiative emission spectrum. We must remember that Figure 6 is deceptive for this purpose because the amplitude of the solar insolation spectrum and the Earth emission spectrum have been normalized. It is also deceptive because the abscissa is not the energy scale we would desire for our purposes, but it is the logarithm of the wavelength. Because the energy of a photon is proportional to the inverse of the wavelength, this means the energy scale on the solar spectrum side is compressed, while the energy on the Earth emission side is expanded. When we look at the absorption of carbon dioxide below that of water vapor, the same distortions apply. Such plots are one of the reasons why so many scientists dismiss the importance of both water vapor and carbon dioxide absorption of incoming solar insolation and over-emphasize that of their absorption of the Earth's radiative emissions.
How do we adjust the amplitude of the solar insolation spectrum. Let us compare the solar insolation that passes into the atmosphere minus that reflected from the atmosphere to the surface emission. Using the K-T energy budget of Figure 2, the solar insolation into the atmosphere is (342 - 77) = 265 W/m2 and the surface emission should be (168 - 24 -78) W/m2 = 66 W/m2 . The ratio of the integrated areas under the curves, if they were plotted on an energy scale would then have to be about 265 / 66 = 4.02. For the moment, let us forget the problem of the abscissa not being linear in energy. We will just multiply the amplitude of the solar insolation curve by a factor of four.
Now let us examine the CO2 absorption plot by itself. Observe the four most intense peaks and note that if we have multiplied the amplitude of the solar insolation curve by four, then the third of the four largest CO2 absorption peaks from the left side has about the same effect on both the solar insolation spectrum and on the surface emission spectrum at about 287.65K. We will amplify the magnitude of the CO2 absorption peaks to its left by a factor of four. Comparing the four-fold increased area of those peaks in the energy range for the solar insolation with those in the surface emission energy range, one finds that the energy absorbed by CO2 from the solar insolation is about 1.3 times that absorbed from the surface emission spectrum. What is more, because the energy ranges on the solar insolation side are compressed and those on the surface emissions side are stretched, this is an under-estimate. CO2 by itself is clearly doing more to cool the surface by keeping solar energy from reaching it, than it absorbs on the emission side.
We also have to remember that even if the energy absorbed from the sun were equal to that absorbed from the surface, the effect would still really be a cooling of the surface. This is because of a built-in asymmetry in the energy transport processes. Contrary to the popular misconception, energy absorption by CO2 from the radiation in the surface emission spectrum does not warm the surface as we have discussed. This absorbed energy is doomed to follow the same path as the energy absorbed by the atmosphere out of the incoming solar insolation. That energy will percolate upward and be emitted from higher up in the atmosphere without affecting the surface temperature.
The Mean Atmospheric Radiative Altitude
There is
another reason to believe that radiative cooling from the surface is a minority portion of the total cooling. This is
the very stability of the daily cycle temperature range we generally
experience. The more surface cooling is
accomplished by slower energy transport mechanisms such as air conduction and
convection and water evaporation, the more moderate our daily temperature
excursions. If radiative cooling near
the surface really averaged out at 79% of all of the cooling as the K-T energy budget of Fig. 2. claims, the
day to night temperature variations would surely be larger than they are.
Absorption Effect of Atmospheric CO2 on Solar Insolation Compared to Surface Radiative Emission
Absorption Effect of Atmospheric CO2 on Solar Insolation Compared to Surface Radiative Emission
Let us examine Figure 6 to determine what the relative effects of CO2 absorption are on the solar insolation spectrum and on the Earth radiative emission spectrum. We must remember that Figure 6 is deceptive for this purpose because the amplitude of the solar insolation spectrum and the Earth emission spectrum have been normalized. It is also deceptive because the abscissa is not the energy scale we would desire for our purposes, but it is the logarithm of the wavelength. Because the energy of a photon is proportional to the inverse of the wavelength, this means the energy scale on the solar spectrum side is compressed, while the energy on the Earth emission side is expanded. When we look at the absorption of carbon dioxide below that of water vapor, the same distortions apply. Such plots are one of the reasons why so many scientists dismiss the importance of both water vapor and carbon dioxide absorption of incoming solar insolation and over-emphasize that of their absorption of the Earth's radiative emissions.
How do we adjust the amplitude of the solar insolation spectrum. Let us compare the solar insolation that passes into the atmosphere minus that reflected from the atmosphere to the surface emission. Using the K-T energy budget of Figure 2, the solar insolation into the atmosphere is (342 - 77) = 265 W/m2 and the surface emission should be (168 - 24 -78) W/m2 = 66 W/m2 . The ratio of the integrated areas under the curves, if they were plotted on an energy scale would then have to be about 265 / 66 = 4.02. For the moment, let us forget the problem of the abscissa not being linear in energy. We will just multiply the amplitude of the solar insolation curve by a factor of four.
Now let us examine the CO2 absorption plot by itself. Observe the four most intense peaks and note that if we have multiplied the amplitude of the solar insolation curve by four, then the third of the four largest CO2 absorption peaks from the left side has about the same effect on both the solar insolation spectrum and on the surface emission spectrum at about 287.65K. We will amplify the magnitude of the CO2 absorption peaks to its left by a factor of four. Comparing the four-fold increased area of those peaks in the energy range for the solar insolation with those in the surface emission energy range, one finds that the energy absorbed by CO2 from the solar insolation is about 1.3 times that absorbed from the surface emission spectrum. What is more, because the energy ranges on the solar insolation side are compressed and those on the surface emissions side are stretched, this is an under-estimate. CO2 by itself is clearly doing more to cool the surface by keeping solar energy from reaching it, than it absorbs on the emission side.
We also have to remember that even if the energy absorbed from the sun were equal to that absorbed from the surface, the effect would still really be a cooling of the surface. This is because of a built-in asymmetry in the energy transport processes. Contrary to the popular misconception, energy absorption by CO2 from the radiation in the surface emission spectrum does not warm the surface as we have discussed. This absorbed energy is doomed to follow the same path as the energy absorbed by the atmosphere out of the incoming solar insolation. That energy will percolate upward and be emitted from higher up in the atmosphere without affecting the surface temperature.
The Mean Atmospheric Radiative Altitude
If radiative cooling from the surface is a large fraction of the Earth’s total cooling, one would not expect the space radiative equilibrium temperature of 255K to be found at the upper part of the water high concentration zone and near the upper end of its 4500 m to 6500 m direct emission range into space. One would have a weighting of the water emission altitudes with the surface in which the surface would enjoy an advantage due to its higher emission temperature and expect a lower top to the portion of the atmosphere not in radiative equilibrium with space. Consequently, the altitude at 255K would be lower than that we find it at, namely 5105 m interpolating from the U.S. StandardAtmosphere Table of 1976.
Indeed, it is interesting to calculate the mean altitude from which water vapor would emit most of the Earth’s IR radiation off into space. We know that the Earth radiates about 235 W/m2 of IR radiation into space. The direct radiation emitted from the surface into the atmospheric window and which is the only radiation from the surface seen in space is about 40 W/m2 according to K-T. Subtracting this from the total Earth IR emission of 235 W/m2 we find that the top of the water vapor layer emits almost all of the remaining IR radiation into space, which is 195 W/m2. The portion emitted by carbon dioxide will come from higher altitudes than that from water vapor does on average. Since the U.S. Standard Atmosphere puts the altitude with the temperature of 255.0K at about 5105 m, we can calculate the effective mean IR-emitting gas radiation altitude needed to make this so. Let us call this altitude H, then
[(195 W/m2) / (235 W/m2)] H = 5105
m
H = 6150 m
An effective mean IR-emitting gas altitude
for the IR photons emitted into space of 6150 m seems to be a reasonable
value. If it is, then we can understand
why the mean radiative weighted altitude between direct surface IR radiation and the
IR-active gas radiation is about 5105 m.
Surface Absorption of Back Radiation
Real materials on the Earth's surface do not absorb all infra-red radiation in the mid and long wavelength range equally or with 100% absorption as imagined by the K-T Energy Budget. If they did, FTIR spectroscopy would not be the powerful laboratory spectroscopy that it is for identifying many different materials based upon their widely differing responses in absorbing infrared radiation of different wavelengths. If the actual materials on the surface of the Earth absorbed as black body radiators do, there would be no peaks in the absorption spectra such as will be seen in the materials spectra to be shown. The spectra of absorption would be very uninteresting and be just a long gentle curve across the entire spectrum and absorption levels would be very much higher.
Let us consider some infrared absorption spectra of materials found on the surface of the Earth and compare them to those of water vapor and carbon dioxide to see another reason why the surface does not absorb all of the mid and far infrared radiation incident upon it from the atmosphere and why it is better at absorbing the emissions of water vapor than the emissions of CO2. Most of the Earth’s surface (71%) is covered with liquid water. Water does a pretty good job of absorbing IR radiation emitted by water vapor, since the emitter and the absorber are well-matched in their emission and absorption wavelengths. Minerals and soils on land often are moist or have waters of hydration within the crystal structure of included inorganic compounds. Plants are full of water. As we will see, the same cannot be said many surface materials with respect to CO2.
Surface Absorption of Back Radiation
Real materials on the Earth's surface do not absorb all infra-red radiation in the mid and long wavelength range equally or with 100% absorption as imagined by the K-T Energy Budget. If they did, FTIR spectroscopy would not be the powerful laboratory spectroscopy that it is for identifying many different materials based upon their widely differing responses in absorbing infrared radiation of different wavelengths. If the actual materials on the surface of the Earth absorbed as black body radiators do, there would be no peaks in the absorption spectra such as will be seen in the materials spectra to be shown. The spectra of absorption would be very uninteresting and be just a long gentle curve across the entire spectrum and absorption levels would be very much higher.
Let us consider some infrared absorption spectra of materials found on the surface of the Earth and compare them to those of water vapor and carbon dioxide to see another reason why the surface does not absorb all of the mid and far infrared radiation incident upon it from the atmosphere and why it is better at absorbing the emissions of water vapor than the emissions of CO2. Most of the Earth’s surface (71%) is covered with liquid water. Water does a pretty good job of absorbing IR radiation emitted by water vapor, since the emitter and the absorber are well-matched in their emission and absorption wavelengths. Minerals and soils on land often are moist or have waters of hydration within the crystal structure of included inorganic compounds. Plants are full of water. As we will see, the same cannot be said many surface materials with respect to CO2.
Fig. 7. The absorption
spectrum of a pool of tap water is shown here taken on an FTIR instrument at 4 cm-1
resolution using the attenuated total reflectance (ATR) mode. The ATR mode limits the sampled depth or attenuation depth into the water to about 1 to 2 micrometers at its surface. Liquid water absorbs IR radiation at certain
wavelengths capable of exciting vibrational modes in the bonds of its molecule. The
spectrum above of absorption in a thin layer of water is clearly
nothing like that of a black body absorber. In a deep body of water,
the fact that below 3700 cm-1
wavenumbers the absorption is always greater than zero allows considerable
absorption to occur in the first ten meters or so of the water body.
Real bodies of water commonly also have many scattering particulates in
them, so some IR is also scattered off such particulates back to the
atmosphere. Furthermore, the water temperature commonly drops with
depth at a rate that commonly exceeds the drop in temperature with
altitude in the air just above the water surface. This means that IR
absorbed in the several meters beneath the surface cannot be absorbed by
the warmer air a couple of meters above the water surface. Note that 4000 cm-1 is 2.5 µm,
2000 cm-1 is 5 µm, 1000 cm-1 is 10 µm, and 400 cm-1
is 25 µm. Divide 10,000 by the
wavenumber to get the wavelength in micrometers. The water peaks here are at 3300 cm-1
(3.0 µm or 3000 nm) and at 1634 cm-1 (6.1 µm). The broad peak at 3.0 µm is in the very low
energy tail of the Solar emission spectrum and the low intensity, but high energy portion of the Earth’s emission spectrum, while the peak at 6.1 µm is near
the peak in the Earth’s emission spectrum, but not nearly as wide as the water
vapor absorption peak claimed in Fig. 6.
Beyond 25 µm in the Earth’s surface emission spectrum water vapor absorption
in the atmosphere or in much of the Earth’s surface is commonly quite complete. Beyond 25 µm of the Earth’s surface emission
spectrum, one is in the low energy tail of that spectrum. Note that water does not absorb IR radiation
emitted by water vapor with total efficiency.
The peak at 3300 cm-1 is absorbing about 53% of the radiation
incident on it at its peak, while that at 1634 cm-1 it is absorbing 34%
of the incident radiation at its peak.
These values may not be the same for back radiation, but they also will
not be totally efficient absorption.
In comparison, the spectrum of CO2 at a concentration in air many, many times that of the atmosphere is shown here in transmission mode in the upper spectrum of Fig. 8. The lower spectrum of Fig. 8 shows the effect of increasing the concentration of CO2 many times beyond the saturation of the main absorption peak so that a couple of weak absorption peaks can be seen clearly. Now note that the range of wavelengths over which CO2 absorbs infrared radiation is much more limited than the range over which water does.
Fig. 8. The absorption spectrum of CO2 at many times the concentration of the atmosphere is shown. The carbon dioxide concentration in the lower image is much higher than that in the upper image. Note that there is little absorption in the water spectrum where the main CO2 absorption doublet peak at about 2345 cm-1 (4.26 µm) is. Much weaker absorption and emission peaks are found at 3723, 3614, and 664 cm-1 or at 2.69, 2.77, 15.06 µm where the last is the most significant in the low temperature emission spectrum of the Earth. This weaker, but important absorption peak, corresponds to the rising edge of the very long wavelength continuum of water absorption. Water vapor absorption is not commonly saturated at this wavelength between the ground and space, so this is where CO2 is supposed to have its primary effects as a greenhouse gas. It is also the emission peak energy at which water in the surface of the Earth will primarily absorb energy emitted by CO2 molecules in the air. The weak features in the lower partial pressure spectrum of CO2 which do not enlarge in the higher pressure spectrum are likely due to the lowered ratio of CO2 to water vapor in the analyzed air path. This is likely because of dimers or trimers of CO2 and water molecules in complexes. This is not surprising given that such complexes are found in the spaces of interlamellar lattice structures in many minerals.
Of course, much of the land surface is covered by vegetation, soil, and minerals. Let us examine a few sample spectra for such materials.
Fig. 9. The infrared
absorption spectrum of a green grass blade is shown. Note that the blade is full of water whose
characteristic peaks are readily seen.
Consequently the blade absorbs radiation emitted by water vapor well,
but note that there is little absorption where the main peaks of CO2
infrared emission are at about 2345 cm-1, so the grass blade is a
comparatively inefficient absorber at that wavelength. It is a better absorber at 664 cm-1
or 15.1 µm.
Fig. 10. The infrared absorption spectra of a green bush
leaf (upper) and a very brown fallen oak leaf (bottom) are shown. The green leaf absorbs IR from water vapor
better than the brown leaf, but both absorb that IR radiation much better than
they do that at the wavelength of the most characteristic CO2
emission. The 15.06 µm CO2
absorption more excited by the Earth’s emission spectrum, will be fairly well
absorbed, but with much less than 100% efficiency.
Fig. 11. The infrared absorption spectrum of a moist and fairly rich soil is shown in the upper image and that of dry sand is shown in the lower image. The moist soil absorbs water vapor IR emissions much better than carbon dioxide IR emission. The dry sand does not absorb either water vapor or carbon dioxide emissions well, except for part of the long wavelength water vapor emission spectrum.
Fig. 12. From top to
bottom, outer bark of an old oak tree, aluminosilicate mineral, feldspar
mineral, and lime mineral infrared absorption spectra. The bark absorbs water vapor emissions well
because it is full of water. The
aluminosilicate is a lamellar material that has water molecules between between
the layers of Si, Al, and O atoms, so it has a slight absorption capability for
water vapor emissions, most easily seen in the broad peak at about 3300 cm-1. Neither the feldspar nor the lime are very
good absorbers for water vapor emissions, though they absorb somewhat at the long
wavelength end of the characteristic water spectrum. None of these materials is an efficient CO2
IR absorber.
Those portions of the Earth covered with water, wet or moist with water, and covered with life, will have a substantial ability to absorb IR radiation from water vapor in the atmosphere. Areas covered with relatively dry minerals will generally not absorb such water vapor IR emissions well. Generally, the emissions from CO2 molecules are significantly less well absorbed by the materials covering the Earth’s surface than those of water vapor. That fraction of the 15.8 W/m2 upper bound on IR radiation that may be incident upon the surface and absorbed which is due to water vapor emissions is generally going to be absorbed with a higher efficiency than will that part due to carbon dioxide molecule emissions.
We see that the absorption spectra of real materials of the Earth's surface show that they do not absorb IR radiation in the wavelengths emitted by a real black body radiator at 288K as a black body would. The absorptions would not show peaks, but only a broad curve across the entire spectrum if these materials behaved as black body absorbers do. If they do not behave as black body like absorbers, then they should not act as black body radiators. According to Kirchoff's Law, the absorptivity and the emissivity of a black body like radiator must be equal. It therefore should not be surprising that the effective emissivity that we calculated for the Earth's surface was about 0.5, rather than a value near 1, which a black body would have.
As we have seen, the upper limit on the amount of back radiation is low, especially when compared to the extremely hyped value of the K-T energy budget of Figure 2. Realistically, the back radiation is much lower than the upper limit. Given the usual temperature differential over a mean free path for absorption in the bottom 4 km of the atmosphere, the amount of energy transported in the upward direction by radiation in most cases is very small. Temperature inversions do occur and not too infrequently. Sometimes this allows a net flow of energy downward, but not usually. We have seen the absorption spectra of many of the materials found on the Earth's surface and they cannot absorb all of the energy that is incident. That energy must be reflected. It will soon be re-absorbed by IR-active molecules in the atmosphere.
The Net Cooling Effect of So-Called Greenhouse Gases
Variations in water vapor concentrations in the atmosphere are not only more important than those of CO2 because there is so much more water vapor than CO2, but also because much, much more of the Earth’s surface has a much higher IR absorption efficiency for water vapor emissions than for carbon dioxide emissions. The high preference of surface absorption for IR emissions from water vapor compared to that from CO2 is not recognized in most accounts of how the greenhouse effect is supposed to work based upon back-radiation and how man’s use of fossil fuels is supposed to result in catastrophic warming.
Let us recall that the near infrared absorption of the atmosphere of solar insolation due to water vapor and carbon dioxide was about 65.0 W/m2. This was energy which the IR-active gases have kept from reaching the surface directly and warming it. Compare this to the upper limit of 15.8 W/m2 for mid and far infrared back-radiation incident upon the surface from greenhouse gases in the atmosphere. It is clear that the net effect of the IR-active gases in the lower troposphere not in radiative equilibrium with space is a cooling effect! Since mid and far infrared surface absorption is not totally efficient and we already have reason to believe that this upper limit is a generous upper limit, this cooling effect is significantly larger than the 49.2 W/m2 difference between these numbers.
To be sure, this does not separately address the effect of additional carbon dioxide in several respects. First, the atmospheric absorption shielding of the surface from solar insolation does not separate out carbon dioxide from water vapor or ozone absorption effects. Second, we do not have data on the extent to which the effect of added carbon dioxide shielding is saturated versus the degree of saturation with respect to any back radiation effect. Both are near saturation, but is there just enough imbalance in the degree of saturation that added CO2 will create some small shift in the blocking versus the back radiation effects for that added amount. Insofar as a positive feedback of added warming due to water vapor is invoked to add to the miniscule CO2 effect even when that effect is highly exaggerated, it seems clear that added water vapor is not a highly saturated effect in terms of blocking incoming solar radiation. The overall blocking versus back-radiation power densities make it pretty likely that if added CO2 increased the temperature and increased water vapor, then the water vapor increase will provide offsetting cooling. The water vapor feedback is surely negative rather than positive as required by the IPCC to claim a significant warming effect due to added CO2.
What we have found is that the picture of a large back radiation warming of the Earth’s surface as given by the Kiehl-Trenberth energy budget diagram of Fig. 2 is a very unphysical and wrong view of the real energy budget. If there is any significant warming of the Earth’s surface due to having an increase in the concentration of carbon dioxide, it is not due to increased back radiation. It is certain that the effect of increased water vapor in the lower atmosphere is actually a cooling effect during the daily cycle, though increased water vapor can provide a decrease of night-time cooling, thereby being a warming effect at night. But, due to the failure of the Earth’s surface to absorb the IR emission of CO2 as readily as that of water vapor, it is clear that an increase in CO2 will not have as large a warming effect at night as does water vapor on a per molecule basis.
Discussion of Added Carbon Dioxide Effects in the Upper Troposphere and the Tropopause
One way an increase in the concentration of CO2 in the atmosphere may have a warming effect on the Earth’s surface is to move the altitude of effective radiative equilibrium with space outward so that the gravitational temperature gradient in the atmosphere operates over a longer range so the surface temperature is raised. It would have to do this by increasing the net radiative cooling at high altitudes. Thus even neglecting the negative feedback responses to moving the equilibrium shell outward, an increase in temperature at the Earth’s surface of 1 K or 1ºC would require an increase in the CO2 concentration to increase the effective shell altitude by 154 meters given the static equilibrium temperature gradient of 6.49K/km. Actually more because increased CO2 would also decrease the solar insolation directly absorbed at the surface or at the top of the water vapor IR emission layer.
The Earth’s surface emits radiation into space directly through the atmospheric window. Water vapor is most prevalent at altitudes below its freezing temperature, which occurs at the altitude of about 2300 m. Yet there is enough water vapor above this altitude that almost all of its emission of IR radiation into space from the atmosphere is from altitudes of about 2500 to 6000 m, so this majority IR-emitter emits at much warmer temperatures than does the relatively rare CO2 molecule, which emits from altitudes of about 9,000 to 20,000 m. Because of its lower radiative temperature, its smaller characteristic frequency ranges, and its rarity, CO2 provides a relatively small portion of the radiative cooling of the planet as a whole. Water vapor is the dominant greenhouse gas molecule by virtue of its much greater concentration, its shorter re-emission time, its wider range of absorption and emission frequencies, and its tendency to form dimers and trimers with other atoms or molecules to give it a still wider range of absorption and emission frequencies.
There are also negative feedbacks to added CO2 causing the effective radiative balance point to effectively move to higher altitudes. One of these is the fact that the important issue with respect to the gravity induced temperature gradient is where do fast radiative heat transfer mechanisms become dominant over the slow heat transport mechanisms of evaporation and water transport, air conduction and convection, and winds. This altitude is already determined by water vapor. Adding CO2 at altitudes above water vapor’s emission altitudes, simply has very little effect on the net rate of radiative heat transport. CO2 mostly absorbs radiation where water vapor does and just relays it along. Of course, any decrease of radiation into space is counteracted by the increase in the numbers of CO2 emitters and by any warming of the atmosphere from which it emits due to any decreased radiation cooling efficiency by CO2. There will be whatever adjustments are needed to maintain the radiative equilibrium with space. To date, increasing CO2 concentrations have not produced measurable temperature increases at 8 to 12 km altitude. This is actually evidence that there is no effect of decreased radiation into space due to higher CO2 concentrations.
Consequently, an argument based on the gravitational temperature gradient will not work. What is more, one has to allow that more CO2 in the upper atmosphere should mean more absorption of the IR portion of the incoming solar insolation and that is surely a cooling effect upon surface temperatures.
Another version of the idea is that more CO2 at altitudes of 8 to 12 km would cause CO2 to emit less IR radiation into space because the zone of atmospheric transparency for the main CO2 emission wavelength would rise to a higher altitude of cooler gas. The radiative efficiency of the CO2 would decrease and the entire atmosphere would simply and directly warm up for that reason. This version of a high altitude effect has CO2 serving as a less effective coolant than the version of the preceding paragraphs.
It is claimed that a doubling of the CO2 concentration will cause an increase in the surface temperature of 1.2 K due to a decrease in the radiative cooling of the atmosphere of 3.7 W/m2. This cooling decrease is based on the foolish assumption that all of the surface warming since the end of the Little Ice Age is due to an increase in the concentration of CO2 in the atmosphere. Note that the 1.2K increase due to doubling the CO2 concentration is that predicted due to CO2 increasing alone and does not include the IPCC prediction of a total 5.4K increase due mostly to a positive feedback due to increased water vapor, for which there is no evidence either.
The general circulation climate models predict a slight warming of the 8 to 12 km altitudes over the Equator and the lower latitudes, but this has not been found to be the case. There is as yet no clear evidence that increasing CO2 is actually re-structuring the atmosphere in such a way as to significantly move the shell of effective radiative equilibrium with space or to change the overall temperature of the upper troposphere.
However, satellite measurements of Earth emission data shows that the IR photons absorbed by CO2 molecules are not re-emitted before the energy gained is redistributed by collisions with other non-greenhouse gas molecules. We know this because the re-emission of radiation does not occur at a black body temperature of 288K and instead occurs at a black body temperature of about 210 to 220K characteristic of general air temperatures at altitudes from 10.5 km to 22 km. [See Fig. 8.3 of A First Course in Atmospheric Radiation, First Edition, Grant W. Petty, Sundog Publishing, Madison, Wisconsin for such measured spectra and observe the CO2 absorption region of 15 micrometers wavelength. This is a weaker emission line than the primary emission line, so it is less subject to saturation at a lower altitude. The main emission line will not have its final emissions into space from a lower altitude, but will be higher if anything. There is a similar spectrum in Fig. 25 of the Ermecke paper.]
This is an important contradiction of the claim that CO2 emission into space is primarily from 8 to 9 km in altitude as is sometimes claimed. Because from 11 km to 20 km the temperature is almost constant at 217K, this being the tropopause, more radiation from this altitude is not important from the standpoint of moving the overall altitude of effective radiative equilibrium with space. The supposition that increasing the CO2 concentration will cause CO2 emitters to emit at a lower temperature into space and decrease the overall radiative cooling is wrong.
One way or another, the planet as a whole has to be in radiative equilibrium with space. As long as the radiative energy inputs of space do not change, the radiative response of the Earth must equal that input. As we have seen, the surface temperature is determined by the absorbed solar insolation and the range over which non-radiative energy transport plays a major role. If there is a decrease in the radiative output of CO2 in our atmosphere at altitudes higher than those in which other transport mechanisms are important, then the net radiation output of other IR-emitting molecules must increase to compensate for that decrease attributed to CO2. Since water is the dominant IR-emitter, any change in the CO2 power emission into space will invoke an equal and negative feedback from water vapor.
Note that such a negative feedback need not apply in the near surface atmosphere where the atmosphere is not in radiative equilibrium with space. It must apply to the Earth’s radiation into space, barring a small caveat for other energy couplings with space such as the solar wind, debris entering our atmosphere, and couplings of the Earth’s magnetic field to the sun’s magnetic field. The small heat flow from the Earth’s deep interior is also another small, but genuine, heat source. However, the sun is by far the dominant and controlling heat source and the Earth is for most practical purposes simply in a radiative equilibrium, albeit over a substantial period of time due the great heat capacity of the oceans, the Earth’s land surface, and to a lesser extent the atmosphere.
Conclusions
The bottom line is this: There is no reason to believe that increased CO2 in the Earth’s atmosphere, whether due to man’s use of fossil fuels or a general decrease in its solubility in oceans still slowly warming since the end of the Little Ice Age, will cause an increase in the surface temperature of the Earth. In fact, it is more likely to cause a small decrease in the surface temperature due to increased atmospheric absorption of incoming solar insolation in the near infrared.
It is clear that the net effect of the IR-absorbing gases now in our lower atmosphere is a surface cooling effect, yet is also true that without water vapor in our atmosphere and a dense lower atmosphere of infra-red inactive gases, the necessary conditions would not exist to keep the Earth’s surface from being in radiative equilibrium with space. This would mean that the surface temperature would be much cooler on average with disastrous temperature cycles during the daily cycle. Actually so much would be different that the surface temperature of the Earth would behave much like that of the moon. Thus it is correct to say that IR-active water vapor warms the Earth’s surface as an essential part of the complex mechanism that allows the surface to be substantially warmer than it would be in direct radiative equilibrium with space.
Yet, it is very important to know the context in which this is true and to understand that carbon dioxide does not have the strong effects of water vapor. In fact, it is probably a coolant in all respects. Water and water vapor act as coolants and warming agents within the framework of an Earth covered with water and surrounded by a thick, predominantly IR-inactive atmosphere of gases. Their roles are complex and fortunately act within a very reliable and stable set of feedbacks that moderate changes in the Earth's surface temperature.
Increased carbon dioxide concentrations in the atmosphere are actually good for plants and all the animals that rely on plants. Most plants evolved under conditions of much higher carbon dioxide concentrations in the atmosphere and thrive with more of the carbon dioxide that is essential food for them. Greenhouse operators have long greatly increased the carbon dioxide concentrations inside their greenhouses to get very substantial increases in plant growth, flowering, and fruit production.
Professor Cliff Ollier has presented an excellent discussion of the effects of added atmospheric carbon dioxide upon plants and animals of the oceans. Marine animals such as coral and shellfish that use carbon dioxide for protective housing thrive with higher concentrations of carbon dioxide. The claim that such higher concentrations of atmospheric carbon dioxide will cause the oceans to become acidic is false. Coral and shellfish have actually been so effective in converting carbon dioxide into limestone sediments over the eons that they are responsible for the Earth having too little atmospheric carbon dioxide now for the good of plants and animals.
It is also necessary to note that the claim that increasing CO2 concentrations in the atmosphere mean a catastrophically increasing surface temperature is based on a very poor understanding of and application of physics. The fact that so many professional science organizations have claimed that the catastrophic man-made global warming hypothesis is now settled science is a disgrace. In addition to the many problems with the physics used to support the hypothesis of catastrophic effects, there is a long history of geological evidence that high CO2 concentrations in the atmosphere do not cause warming and catastrophic conditions that have threatened plants and animals. The evidence is that the climate is fairly stable and much more affected by changes in solar insolation and cosmic ray nucleation of clouds than by CO2 concentrations. There is a predominance of evidence that warming results in increases in the atmospheric CO2, rather than the other way around. Contrary to the suppositions of the catastrophic warming hypothesis, there is even evidence now that the warming since 1982 preceded increases in atmospheric CO2.
There are also many sad instances in which the warm periods of the historical past have been manipulated out of the scientific record. The warm 1930s have been artificial jiggered to cooler temperatures, as has most of the surface temperature data between then and about 1975. Somehow urban heat island effects were more in need of correction when the human population was smaller than it has been in this most recent period back to 1980. Then there is the loss of many rural weather stations since in the surface temperature records and much evidence that temperatures measured by rural stations did not show significant increases. The Medieval Warming and the Roman Warming were all minimized. Proxy temperature data was often manipulated to minimize the temperatures of prior warm periods.
Scientists who have gone along with this theory of catastrophic effects caused by carbon dioxide emissions have been rewarded with over $100 billion of research money by the U.S. Government or additional money from other governments. By giving many politicians more excuses for expanding the role of governments in controlling their people, businesses, resources, and the standard of living of their people, many posing as scientists have become handmaidens to tyranny. Handmaiden is a nice way of saying what these scientists and scientific organizations have really become. This is, of course, a betrayal of science by many who are supposed to be dedicated to its rational, objective, and critical thinking requirements.
This post was first posted on 17 February 2013 and continued to be updated frequently until 7 April 2013. Additional comments were added on 1 June 2014. Still further comments were added on 10 and 12 August 2014 [relating to near-IR infra-red absorption and emission by neutral atoms of N, O, C, and Ar resulting from a comment below by MS]. I added to the section The Black Body and the Earth Radiator before Fig. 2. to clarify why the radiative emissivity of the Earth's surface is about 0.48 or 0.5 and not near 0.95 as so many claim on 20 January 2015. Further minor editing was done on 7 March 2015 and on 28 April 2015. Additional comments were made on 22 May 2015 referring to my post The Greenhouse Gas Hypothesis and Thermal Radiation -- A Critical Review. Further changes were made on 30 November 2015.
This paper is available in .pdf format and will be sent upon request.









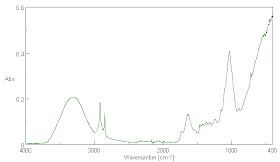






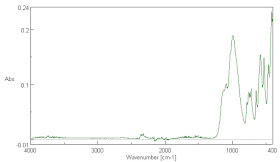

Why don't you publish this paper in a peer-reviewed journal?
ReplyDeleteWhile parts of this article are original in their viewpoint, much is not and has been published by others.
ReplyDeleteThe physics is almost too simple to be published in a professional journal, yet few of the reviewers of the climate journals would be capable of understanding that simple physics.
The reviewers of the climate journals are selected to be adamant supporters of catastrophic man-made global warming. Those supporters are not open to reason.
I have a laboratory to run and this is an aside which I do as part of my need to defend science and liberty from abuse.
The article is not written as a review paper and it is not written as a report on new research. It does not fit the genre of a peer-reviewed paper. It is written to convince a rational person with a modest understanding of science that catastrophic man-made global warming does not make sense. It does not use the expected jargon of professional climate scientists, and such scientists really dislike that.
quote:
ReplyDeleteMuch of the absorbed energy is re-emitted as UV radiation and half of that energy is quickly lost to space. Nonetheless, much of the UV light energy is absorbed by the ground. In addition to the absorption of UV by ozone.
/end quote
I have several questions regarding this line.
Since Sun and ozone aren't in thermal equilibrium how is it possible for a gas at a temperature -40°C to emit UV light? According to Planck Law a black-body at this temperature would peak somewhere in around 10um and then curve rapidly falls down to 2um where it emits very little. So how is it possible for ozone to emit so much in UV? Shouldn't gas first absorb the energy and then if not in thermal equilibrium with the source (Sun) heat up and emit at wavelengths that correspond to its temperature and emission specter? Could this be because ozone is not in local thermal equilibrium with other ozone molecules?
Much of the UV light absorption occurs at sufficiently high altitudes that the collision frequency is much reduced relative to that in the lower troposphere. As a result, an excited state has a much greater probability of de-exciting with radiative emission and much less likelihood of losing absorbed UV radiation energy by means of molecular collisions. So, yes, it is because the absorbing molecules of ozone are not in thermal equilibrium with other molecules.
ReplyDeleteThank you for your answer, i got another question now.
ReplyDeleteCan a single atomic gas or any other matter heat up (so we can measure it with thermometer) just with electronic transitions? Im asking this because i was reading somewhere that only vibrational and rotational transitions can transfer energy in non-radiative manner. This suggests that even though single atoms absorb radiation with electronic transitions they are incapable of transmitting this energy in a way that would increase their kinetic energy and thus increase gas temperature.
Again thank you for your time,
Regards
The chief monatomic gas in our atmosphere is argon. Argon has a concentration of about 0.93%. There is also atomic oxygen at higher altitudes.
ReplyDeleteArgon has many ionization potentials, the lowest of which is 15.759 eV. Oxygen's lowest ionization potential is 13.618 eV. In either case, this is a lot of energy to transfer to a single atom. But let us suppose that the atom has become electronically excited by UV radiation, so the conservation of momentum requirement causes very little perturbation of the atom's momentum, since photons have nearly zero mass and small momentum. Not zero momentum mind you, but this effect on the translational energy of the atom is very small.
So we must then consider the electronic transition upon radiative de-excitation of the atom. This de-excitation is by the emission of a photon so the momentum change of the atom is very small. So far what you have been told seems nearly enough correct. However, there is an alternative means of de-excitation of the excited atom. This is by means of the emission of an Auger electron. This de-excitation process involves 3 electronic levels and may involve a cascade process that affects still more electronic levels. One or more electrons are emitted and they now have a significant mass compared to a photon. Momentum conservation does require that the translational energy of the atom be altered. But this process is randomized over many such emission processes in terms of the direction of emission relative to the translational velocity of the atom. So the affect on any significant gas volume is likely to be very little. So, again, not much of a temperature change is likely to result.
Now, we have to consider the fact that the excited atom is ionized. We also have to consider the case following Auger de-excitation in which the atom may be missing still more electrons and be even more ionized. In the atmosphere there are often electric fields, such as in clouds and in the stratosphere and above. The excited gas atom can respond vigorously to these electric field potentials and acquire a very high amount of energy in the process. The atom may gain a high velocity and then transfer this energy to other gas molecules upon collisions. This effect is likely to have an insignificant impact on the surface temperature, but it is not correct to say that it is essentially zero.
Charles, great post:
ReplyDeleteThis text says that altitude where decay rate and thermalization rate are equal is ~ 70K
https://books.google.com/books?id=2x4CAQMEKigC&pg=PA324&lpg=PA324&dq=Ir+RADIATIVE+LIFETIMES+water+vapor&source=bl&ots=HN54g5xJRi&sig=BmcexJKIpyn3A385MXgHP7QdGYQ&hl=en&sa=X&ved=0ahUKEwiAsoingrbJAhWIMSYKHTzUDsI4ChDoAQhIMAc#v=onepage&q=Ir%20RADIATIVE%20LIFETIMES%20water%20vapor&f=false
Thanks for your comment Ronald. The 70K looks like a temperature, but you intended that to be an altitude of 70 km. The radiative excitation times are longer than I realized. I will make an update on this in the post above!
ReplyDeleteSorry to be sloppy. Yes the text says 70 km altitude. Well up where the temperature lapse rate curve is inverted and the temperature is even higher than the tropopause.
ReplyDeleteIf this be true, obviously this physics says that CO2 increase will be negative feedback itself let alone not producing a greenhouse warming. I've never been concerned with their 1.5 watt/m^2 greenhouse anyway since I'm convinced that all water vapor which increases the surface temperature will cause increased water vapor which is the primary energy transport and radiation source to space. As such any increase in water vapor is a cooling factor and must be negative feedback to planet energy balance.
Charles, interesting indeed.
ReplyDelete1. Can you please advise where the wrong alarmist idea comes from, that the absorbing gases re-emit half of the IR radiation back to the surface of the Earth:
»The infrared absorbing gases in the atmosphere absorb most of the IR radiation and re-emit half of it into space and half of it back toward the surface of the Earth.«
2. How do you know that the alarmists overstate the back radiation »hugly« and do you know how much is re-emitted ?
»But the alarmists overstate the radiation emitted from the Earth's surface by a factor of two and they overstate the radiation returned to the Earth's surface hugely.«
Examine Fig. 2., the alarmist Earth Energy Budget. According to it, the surface at 288K emits 390 W/m^2 into the atmosphere, which is greatly exaggerated for reasons I explained in this post. The atmosphere absorbs all of that except the 40 W/m^2 that they claim passes through the atmospheric window into space. In reality, there is no way that the atmospheric window allows only 40/390 = 0.103 of the surface emitted IR to reach space. According to Fig. 2, the atmosphere radiates 324 W/m^2 of infra-red radiation to the surface because of the heat in the so-called greenhouse gases. Infra-red absorbing gases will re-emit infra-red in all directions equally, not just back to the surface. If they were emitting 324 W/m^2 to the surface, then they would also be emitting 324 W/m^2 to space. Yet according to the Earth Energy Budget of Fig. 2., only 195 W/m^2 is being radiated to space. This is nonsense.
ReplyDeleteIn reality, the temperature of the black body radiating 324 W/m^2 would be 275K. This is the temperature in the U.S. Standard Atmosphere at an altitude of about 2000 meters altitude. By far, the most important infra-red active gas is water vapor, and except in very dry areas of the Earth, such as over deserts and the arctic regions, the absorption length for radiation emitted from water vapor is less than 10 meters. The absorption length for the infra-red radiation emitted by carbon dioxide is certainly less than 50 meters. If infra-red radiation emitted from 2000 meters above the surface were to reach the surface as infra-red radiation, it would have to be at the end of a chain of more than 40 absorptions and re-emissions in the case of CO2 and more than 200 absorptions and re-emissions in the case of water vapor. Even if that could happen, each re-emission would have at least a 50% probability of being in the direction of a higher, not a lower altitude. So, if CO2 emitted radiation from 2000 m altitude is to reach the surface as the result of 40 re-emissions, only (0.5)^40 = 9.1 x 10^(-13) of it would reach the surface. It gets worse, because not one time out of 5 is the energy absorbed in a CO2 molecule re-emitted as IR radiation. It is almost always lost in collisions with other molecules in the air in the lower 2000 m of the atmosphere. So, the likelihood that IR radiated from CO2 at 2000 m altitude will reach the surface is much less than [0.5 (.2)]^40 = 1 x 10^(-40). The at least 200 events required for water vapor to do so makes that probability also exceedingly minuscule.
It is not radiation that is the primary mover of energy from the surface upward through the atmosphere and radiation moves almost no energy downward in the atmosphere. It is air convection and the transport of energy in water vapor and rain that are the dominant means of energy transfer. This is why the altitude at which the atmosphere has the temperature of black body equilibrium with space with the temperature of 255K is 5000 meters in the U.S. Standard Atmosphere. One has to get above 5000 meters altitude before radiation becomes the primary means of energy transport in the atmosphere.
Let me elaborate a bit on the idea that a molecule in the atmosphere emits infra-red radiation isotropically or uniformly in all directions. A central principle of the standard catastrophic man-made global warming model is that every material at a temperature above absolute zero emits thermal radiation exactly as it would if the material surface or molecule were isolated in space with all the rest of space at absolute zero temperature. This is actually false, because photon emission depends upon the electric field around an oscillating dipole which is commonly a many-body physics problem. The thermal radiation emitted from a body is also dependent upon whether that same body has other energy loss mechanisms, such as collisions with other bodies and the evaporation of water. The energy of the oscillating dipoles can only go into photon emission if that same energy has not be used to evaporate water or been transferred to other molecules during collisions.
ReplyDeleteTaking the real electric field gradients, the mean free path between the absorptions of such photons of energy that water vapor and carbon dioxide can absorb, and the other energy loss mechanisms into account, we find that radiation transport of energy is preferentially upward in the atmosphere and only significant downward when there are temperature inversions. There are times when I show that even under the isotropic emission scheme that the catastrophic man-made global warming theory is based upon, they have violated that principle and actually are claiming there is a preferential downward radiation of energy. They have the actual direction of radiative energy transfer from the surface relatively inverted as far as radiation in the atmosphere is concerned. Yes, they maintain a small differential with the surface radiation slightly larger than the back-radiation, but that differential is much, much larger than they maintain it is. In addition, the upward bound radiation within the atmosphere itself should be larger than the downward radiation within the atmosphere.
Dr Anderson, Interesting assessment.
ReplyDeleteI am very much a fan of many of the quotes.
My assessment has about the same conclusion but approached somewhat differently.
Mother Nature does not do politics.
CO2 in the atmosphere only matters to plants.
Thermalization and the complete dominance of water vapor in reverse-thermalization explain why CO2 has no significant effect on climate. Terrestrial EMR absorbed by CO2 is effectively rerouted to space via water vapor.
CO2 is not merely harmless, it is profoundly helpful. It is helpful in that it is plant food and reduces plant’s need for water.
Sunspot number anomaly time-integral plus net of the effect of all ocean cycles plus effect of water vapor increase provides a 98% match to temperature anomaly measurements 1895-2015. Analysis and graphs are at http://globalclimatedrivers2.blogspot.com
Now peer reviewed at http://irjes.com/Papers/vol5-issue11/E5113145.pdf
A looming issue that humanity should be addressing is the decline of water tables where spray irrigation is used.
Great article. Regarding more CO2 in the Upper Troposphere (UT) causing more UT cooling, I agree, but why would that cause the emission altitude to increase (and thus the surface to warm)? It would to the opposite: more outgoing IR at TOA would reduce surface warming (possibly LOWERING the emission altitude, no?
ReplyDeleteMoreover, there is no upwelling 15 micron IR for UT CO2 molecules to intercept, as they've all been extinguished as you say in 100-200m from the surface. Indeed, as you say above that reemission by CO2 is not possible at 288K, therefore all the energy from the first CO2 IR capture (in 15 micron bandwidth) is extinguished and therefore there's no further absorption of surface IR from higher CO2 molecules (because there's none to absorb, duh). As I read that CO2 IR in is capture by CO2 within 33m, then you could revise your "100-200m" value to "33mm" as there's only one capture and no reemission of 15 micron IR upwelling by CO2 molecules.
Therefore the only IR for UT CO2 molecules to absorb are downwelling IR from insolation that happen to be in CO2's absorption bands. This effect is the sun-shade effect you discuss and definitely cools the surface by preventing insolation getting to it.
However I don't buy your argument concerning Figure 6. OF course I understand that the left side (insolation) is understated in terms of energy vs the right side, but that would seem irrelevant because for CO2 IR at least (the crux of AGW alarmism) there's de minimus IR from the down-welling insolation for UT CO2 molecules to intercept IN THE 15 MICRON bandwidth that is relevant.
So your thesis seems to be that IR from the surface is really 66-40 W/M2 and of the 26W/M2 any 15 micron bandwidth is absorbed once and then totally thermalized (because reemission of CO2 at 288K is not allowed) and thus there is no more upwelling CO2 sensitive IR above say 33m (where the first CO2 capture occurs). Above that, CO2 is completely inactive except for a very tiny amount of sun-shade effect in the UT, which in any event will cool the surface.
There's no way the UT CO2 can warm the surface by cooling the UT because: a) that's a contradiction in the first place; and b) the only impact of UT CO2 is sun-shade effect.
This also explains why there's no UT Hot Spot.
This Nasif Nahle gives 32.75m (not 47m) as the mean free path for CO2 photons to collide:
ReplyDeletehttp://www.biocab.org/Mean_Free_Path_Length_Photons.html
The 1.2C warming from 2X CO2 is derived from the 3.71W/M2 [presumed] forcing from 2X CO2, yet
ReplyDeleteThere's less than 1C difference (not 1.2C) between Stefan-Boltzmann energy using 256K vs 255K.
Just using Stefan-Boltzmann a 3.71W/M2 forcing (i.e. that from 2x CO2) only creates a .99C temperature increase .... and that's at 5.1Km.
I believe the 1.2C from 2X CO2 meme is pre-Myhre 1998 when the forcing of 2X CO2 was believed to be 4W/M2 (not 3.71).
Hello Charles.
ReplyDeleteI note that you do say that much of what you say has previously been published by others.
In that connection I found that many sections sounded rather familiar and accorded with my style of exposition.
Did you use any of my work in putting it all together?
Various articles by me covering many of the same points have been published here:
https://www.newclimatemodel.com/
and in many sceptical blogs over the past 12 years.
Hi Stephen,
ReplyDeleteActually, I am very unfamiliar with your work. I will be interested to read more about it.
I have been writing about why I suspected catastrophic man-made global warming theory was wrong since about 2008, originally mostly on Objectivist forums. Mostly, I figured out why it was wrong very much on my own, but I always thought that other scientists were surely also capable of figuring out most of the reasons because it does not take an Einstein to figure them out. Indeed, they are easy enough to figure out that it is clear to me that most of the consensus scientists who really have devoted time to thinking about the effects of CO2 are surely being dishonest or proving that they really do not understand physics.
What is most unique in my analysis is my fundamental examination of thermal radiation theory in which I point out that you cannot ignore the basic electromagnetic field theory as everyone does. That leads to a huge exaggeration of photon fluxes and therefore of absorption events and of back-radiation. The essential characteristic of a black-body radiator is Stefan's Law for the constant energy density of the cavity, not the Stefan-Boltzmann Law of Radiation. A photon flux only flows from a higher energy density region to a lower energy density region. If you use the Stefan-Boltzmann equation as almost everyone does, then one can prove that two parallel plates at the same temperature would create a black body radiation cavity with twice the energy density of Stefan's Law. This is fundamentally why the Earth Energy Budgets all violate the Conservation of Energy and why back radiation is massively exaggerated, as is outgoing radiation from the surface itself. These arguments I have seen nowhere else, though some people make a generalized thermodynamic argument against back radiation. I always thought that argument was somewhat inadequate, though if it is coupled with a minimum energy argument that argument does prove to be right.
I have not been able to write much about these issues lately, since the revived economy in manufacturing since November 2016 has inundated my materials analysis laboratory with work enough to keep me busy 80 hours a week. However, I have accumulated a number of ideas I would like to write about on the subject. The subject should be a dead one, but the alarmists will keep claiming they are right and have a consensus, though they could not be more wrong. They keep calling for catastrophic governmental policies and for companies to waste huge sums of money and talent.
Hello Charles,
ReplyDeleteThere is a section "It is not generally understood among those who discuss man-made global warming that electronic transitions do occur in the near infra-red range from 750 nm to 3000 nm. The emission and absorption spectra for neutral nitrogen, oxygen, argon, and carbon atoms are rich in spectral lines."
In the first place the number of free carbon, nitrogen and oxygen atoms in the atmosphere is negligible. Argon is abundant (93%) so it is a strong absorber. Argon is a closed shell atom so the lowest excited state is very high, absorption at 107.36 nm. The other atoms also have their lowest absorption lines far above the IR range.
You should remove everything about atoms. The end of the section:"Changes in the composition of the atmosphere must take into account the added absorption effects that each of these atoms has on incoming solar radiation by virtue of both electronic transitions and the excitation of vibrational modes in molecules. The added absorption of incoming solar radiation due to increasing carbon dioxide through electronic excitations is a cooling effect upon the surface temperature." is incorrect. Atoms are not involved and there are no electronic transitions in the infrared. All the absorption in the infrared are due to the excitation of vibrational modes in molecules.
Leif, the spectral lines of the NBS tables, edited by Joseph Reader and Charles H. Corliss, I was discussing were not for single atoms accept for argon, but were for their common form in the atmosphere. Thus they were for N2, O2, and CO2. These spectral absorption lines are generally weak, but they exist at least according to NBS, now NIST. There are absorption lines throughout the UV, Visible, and Near Infrared portions of the electromagnetic radiation spectrum.
ReplyDeleteHello Charles,
ReplyDeleteI was astonished by a gaping abyss in the literature of modern physics. Tying up loose ends about radiant energy, I went online for a discussion of Stefan’s Law or Constant. Despite searching by name, by cut-and-pasted formula, and by other devices, I found absolutely no reference on the internet to “Stefan’s Law” or Stefan’s Constant.” Uniformly, sources either simply omit reference or claim it is the same as Stefan-Boltzmann. (Salby cites only Boltzmann and Stefan-Boltzmann among his appendix of physical constants. Wikipedia (hardly reliable) redirects “Stefan’s Law” queries to “Stefan-Boltzmann.” This seems thoroughly Orwellian.)
Your derivation of Stefan’s Law persuades me you are right. It appears so central that, unless “rehabilitated” as the Stalinists used to say, CAGW will get even greater undeserved longevity. It is a subject for at least a paper, with precedents, authority and comments. Has Stefan’s been purged, disproven, superseded by S-B? Is there print authority to support it, such as an early edition of the Handbook of Chemistry and Physics, or others? ...
Thanks,
Tom Anderson, Eureka, CA
Thank you for your comment Tom.
ReplyDeleteAs an undergraduate physics major at Brown University (1965 - 1969), I encountered Stefan's Law for blackbody radiation at least twice. In my sophomore year we used the structure of matter by R.W. Christy and Agnar Pytte which discussed Stefan's Law in Chapter 18 emission and absorption of light. In my junior year we used Thermal Physics by Philip M. Morse which gave it a better discussion in Chapter 7 entitled Simple Thermodynamic Systems. I remember at the time that I thought the Morse derivation very interesting, but even so, there were aspects of its importance that I did not then realize and only came to understand in the years since 2010 as a result of my evaluation of the catastrophic man-made global warming hypothesis.
As with much knowledge, to be applied correctly, one has to know the context for its application. The fundamental property of a black body cavity or a black body radiator is its electromagnetic field energy density, which is given by Stefan's Law. It is then the gradient in the energy density that gives rise to the thermal radiation given by the Stefan - Boltzmann Law. There are many situations for which the Stefan - Boltzmann Law can be applied, so it is widely used and known. The easiest way to apply it is to think that every black body radiator at a temperature T is radiating photons at a power proportional to the fourth power of T, as though it were radiating power to a body at the temperature of absolute zero. This lets one ignore any equilibrium condition that may or may not exist with other bodies at finite temperatures in its vicinity. The photon flux can be much exaggerated, but for many problems one wants to solve, one still gets the right answer in terms of calculating equilibrium temperatures. But the casualty of this calculation method is that the total energy of the system is not conserved -- it is exaggerated. And if your thermal radiation flux can be absorbed by infrared-active molecules, then the cross-section for such absorption will become greater than it really is.
If the two bodies in thermal equilibrium are at fairly similar temperatures such as those at the Earth's surface or in the troposphere, then the photon flux is hugely exaggerated.
One of the commonly used Earth Energy Budgets exaggerates the photon power or flux between the surface and the absorbing and back-radiating atmosphere in the ratio of (117 + 100)/17 =12.76. If you have 12.76 times as many photons flying about then you will have about 12.76 times as many CO2 absorption events and that sure amplifies the effect of CO2! Even then, they get warming effects so small they have to posit positive feedback warming effects by water vapor to get the results they claim represent catastrophic warming. And, as I never tire in pointing out, they ignore the many cooling effects of CO2. They also ignore the fact that they claim the atmosphere can absorb more thermal infrared radiation than a black body at the lowest temperature in the troposphere, tropopause, or stratosphere could absorb, even though the atmosphere has an infrared window and does not absorb at all frequencies across the spectrum. It really is quite crazy.